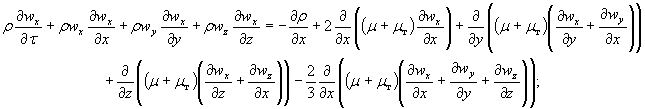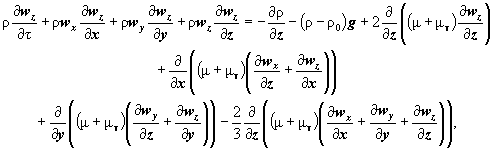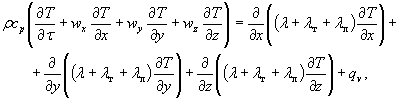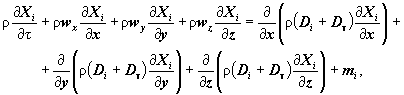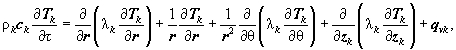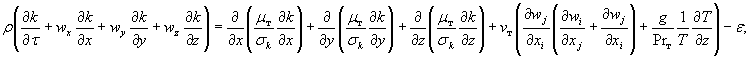|
|||||||||||||||
Все документы, представленные в каталоге, не являются их официальным изданием и предназначены исключительно для ознакомительных целей. Электронные копии этих документов могут распространяться без всяких ограничений. Вы можете размещать информацию с этого сайта на любом другом сайте.
ПРАВИТЕЛЬСТВО МОСКВЫ МОСКОМАРХИТЕКТУРА
РЕКОМЕНДАЦИИ
по оптимизации действия систем
пожаротушения, дымоудаления
и вентиляции при пожарах
2005
ПРЕДИСЛОВИЕ
1. Разработаны Научно-исследовательским институтом Всероссийского добровольного пожарного общества по обеспечению пожарной безопасности (НИИ ВДПО ОПБ): доктор технических наук, профессор Пузач С.В. (руководитель), к.т.н. Чумаченко А.П.
2. Согласованы с УГПС МЧС России г. Москвы, Москомархитектурой.
3. Подготовлены к утверждению и изданию Управлением перспективного проектирования, нормативов и координации проектно-изыскательских работ Москомархитектуры.
4. Утверждены приказом Москомархитектуры от 30.05.2005 № 72
ВВЕДЕНИЕ
В связи с переходом многих стран мира к гибкому объектно-ориентированному противопожарному нормированию математическое моделирование пожаров является определяющим звеном при решении различных задач пожарной безопасности. Федеральное законодательство, в частности, Закон «О техническом регулировании» и стандарт пожарной безопасности (ГОСТ 12.1.004-91), обеспечивают законодательную базу реализации на практике принципа гибкого нормирования.
При решении задач пожаробезопасности (в настоящих Рекомендациях на примере стоянок легковых автомобилей) вопрос точности и надежности метода расчета тепломассообмена при пожаре является ключевым. Сложность разработки такого метода заключается в многофакторности и нелинейности задачи.
Моделирование тепломассообмена при пожаре представляет собой сложную, в полном виде не решенную проблему [5.18]. Реальный пожар как неконтролируемое горение является сложным, до конца не изученным, существенно нестационарным и трехмерным теплофизическим процессом, сопровождающимся изменением химического состава и параметров газовой среды помещения. Турбулентный конвективный и лучистый тепломассообмен в очаге горения с химическими реакциями, теплообмен между горячими газами и ограждающими конструкциями помещения и т.д. осложняются тепломассообменом с окружающей средой через проемы и вследствие работы систем механической приточно-вытяжной вентиляции и пожаротушения, что приводит к существенной неоднородности температурных, скоростных и концентрационных полей продуктов горения в объеме помещения (нестационарность и трехмерность задачи).
О сложности решения такой задачи также говорит тот факт, что математическое моделирование турбулентного тепломассообмена в сложных термогазодинамических условиях вместе с другими задачами нелинейной физики входит в список, составленный Российской академией наук, тридцати особо важных и интересных проблем физики на ближайшие годы [5.19].
В действующей нормативно-технической базе проектирование систем пожаротушения, дымоудаления и механической вентиляции основано на упрощенных методах расчета тепломассообмена при пожаре.
Для определения условий безопасной эвакуации людей необходимым исходным показателем является время критической продолжительности пожара [5.22] (промежуток времени от начала возникновения горения до достижения величины хотя бы одного опасного фактора пожара ее критического для человека значения на уровне рабочей зоны). Однако в российских стандартах безопасности для определения этого времени заложены упрощенные интегральные методы расчета тепломассообмена при пожаре (ГОСТ 12.1.004-91, ГОСТ 12.3.047-98). Использование методов расчета более высокого уровня (зонных и полевых) позволяет более надежно определять величину критической продолжительности пожара.
В действующих нормах пожарной безопасности не учитываются реальные условия пожара, такие как, реальный термогазодинамический режим пожара, теплофизические и химические свойства находящейся в помещении горючей нагрузки, геометрические размеры помещения, размеры и расположение проемов, параметры систем пожаротушения, дымоудаления и механической вентиляции и т.д.
В настоящих Рекомендациях представлена математическая модель, позволяющая на основании научно-обоснованного прогноза динамики опасных факторов пожара проводить оптимизацию действий систем пожаротушения, дымоудаления и механической вентиляции с учетом реальных параметров возникновения, распространения и развития пожара, теплофизических и химических свойств конкретной горючей нагрузки и теплофизических свойств материала строительных конструкций. Методика моделирования основана на современном уровне научных знаний в областях тепломассообмена и вычислительной математики. Методика основана на математической модели, приведенной в [5.48] и прошедшей согласование в ВНИИПО МЧС России. В документе представлены также рекомендации по проведению расчетов систем пожаротушения, дымоудаления и механической вентиляции. За разъяснениями по вопросам, связанным с методикой расчетов, математической моделью и компьютерной программой следует обращаться в НИИ ВДПО ОПБ по адресу: 121357, Москва, ул. Верейская, д.7.
1. ОБЛАСТЬ ПРИМЕНЕНИЯ
1.1. Настоящие Рекомендации разработаны в развитие и дополнение нормативных документов в строительстве, действующих на территории города Москвы, в части обеспечения пожарной безопасности зданий различного назначения.
1.3. Рекомендации распространяются на проектирование систем (п. 1.2) вновь строящихся и реконструируемых зданий различного назначения, кроме производственного.
2. ОБЩИЕ ПОЛОЖЕНИЯ
2.1. В соответствии с Федеральным законом «О техническом регулировании» и требованиями пожарной безопасности (ГОСТ 12.1.004-91, ГОСТ 12.3.047-98 и МГСН 5.01-01) объемно-планировочные и конструктивные решения зданий, в том числе стоянок легковых автомобилей, а также их инженерное оборудование, включающее системы пожаротушения, дымоудаления и механической вентиляции, должны обеспечивать в первую очередь основные требования пожарной безопасности:
- обеспечение безопасной эвакуации людей;
- обеспечение сохранности имущества третьих лиц.
2.2. Настоящие Рекомендации разработаны в помощь проектным и строительным организациям, а также органам пожарной охраны с целью оптимизации действий систем пожаротушения, дымоудаления и механической вентиляции при пожаре в зданиях, в том числе на стоянках легковых автомобилей, с. целью обеспечение безопасной эвакуации людей и сохранности имущества третьих лиц.
Приведенная методика может быть использована при разработке необходимых по законодательству [5.1] технических условий по обеспечению пожарной безопасности зданий различного назначения, кроме производственного.
2.3. В настоящих Рекомендациях представлены основы метода расчета тепломассообмена при пожаре с учетом реальных параметров возникновения, распространения и развития пожара, теплофизических и химических свойств конкретной горючей нагрузки, теплофизических свойств материала строительных конструкций и действий систем пожаротушения, дымоудаления и механической вентиляции. Для более углубленного освоения приведенного метода следует использовать специальную техническую литературу [5.16, 5.18, 5.20].
2.4. Приведенная методика не содержит жестких рекомендаций по применению набора математических моделей, входящих в приведенный метод расчета. Выбор моделей должен осуществляться в соответствии с учетом особенностей конкретного объекта.
2.5. Предлагаемая методика может быть использована для оптимизации действий систем пожаротушения, дымоудаления и механической вентиляции при пожаре, когда горение является дефлаграционным [5.21]. При этом приведенный метод расчета принципиально применим для любого сценария развития пожара.
В случаях взрывного или детонационного горения [5.21] методика требует корректив, заключающихся в изменении моделей горения и конечно-разностной схемы решения.
2.6. В настоящей методике, за исключением специально оговоренных случаев, приняты термины и определения, приведенные в ГОСТ 12.1.033-81 и СТ СЭВ 383-87. Остальные термины и определения, используемые в Рекомендациях, приведены в Приложении 1 к настоящим Рекомендациям. Коэффициенты и постоянные физические величины, используемые в расчетах, представлены в Приложении 2 к настоящим Рекомендациям.
3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
3.1. Расчет тепломассообмена при пожаре с целью оптимизации действий систем пожаротушения, дымоудаления и механической вентиляции является сопряженной задачей теории тепломассообмена.
3.2. Расчет динамики опасных факторов пожара проводится на основе решения трехмерных нестационарных дифференциальных уравнений теплопроводности для многослойной стенки. Граничные условия к этим уравнениям на твердых поверхностях со стороны помещения определяются с помощью трехмерной полевой модели расчета тепломассообмена при пожаре в помещении (сопряженная задача теории тепломассообмена). На наружных поверхностях ограждающих конструкций задаются граничные условия по лучистому и конвективному теплообмену с окружающей помещение средой (наружный воздух, соседнее помещение и т.д.).
3.3. Полевая модель расчета тепломассообмена при пожаре в помещении и математическая модель прогрева строительных конструкций приведена в Приложении 3 к настоящим Рекомендациям.
3.4. Математическая модель в данной постановке может быть решена только численным методом. Метод численного решения математической модели представлен в Приложении 4 к настоящим Рекомендациям.
3.5. Результатом расчета являются рекомендации по оптимизации действий систем пожаротушения, дымоудаления и механической вентиляции в зданиях различного назначения на примере стоянок легковых автомобилей.
4. ОПТИМИЗАЦИЯ ДЕЙСТВИЙ СИСТЕМ ПОЖАРОТУШЕНИЯ, ДЫМОУДАЛЕНИЯ И МЕХАНИЧЕСКОЙ ВЕНТИЛЯЦИИ ПРИ ПОЖАРАХ
4.1. Основные положения по расчету
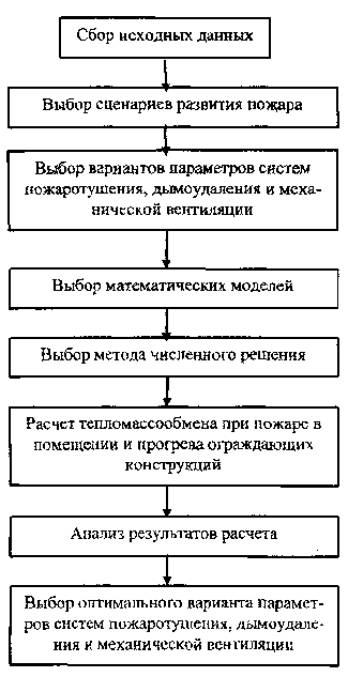
4.1.1. Оптимизация действий систем пожаротушения, дымоудаления и механической вентиляции при пожарах в зданиях, включая стоянки легковых автомобилей, проводится в следующей последовательности:
- сбор исходных данных;
- выбор сценариев развития пожара;
- выбор вариантов параметров систем пожаротушения, дымоудаления и механической вентиляции;
- выбор математических моделей;
- выбор метода численного решения модели;
- расчет тепломассообмена при пожаре в помещении и прогрева ограждающих конструкций;
- анализ результатов расчета.
Блок-схема проведения расчетов представлена на рис. 1.
4.1.2. Сбор исходных данных включает в себя выбор численных значений параметров, входящих в математическую модель (Приложение 3 к настоящим Рекомендациям), с помощью анализа:
- объемно-планировочных решений объекта;
- проектно-конструкторской документации несущих и ограждающих строительных конструкций объекта;
- размещения, вида и количества горючей нагрузки.
4.1.3. По объемно-планировочным решениям и проектно-конструкторской документации определяются геометрические характеристики задачи. Составляется схема привязки к помещению ортогональной системы координат. Выбирается положение центра ортогональной системы координат, например, в левом нижнем углу помещения. Координатная ось х направлена вдоль длины помещения, ось у - вдоль его ширины, ось z - вертикально вдоль высоты помещения.
Рис. 1. Блок-схема проведения расчетов
4.1.4. Определяются следующие геометрические характеристики объекта:
- помещение:
в форме параллелепипеда: длина, ширина, высота;
произвольной формы: координаты поверхностей ограждающих конструкций;
- двери: высота, ширина и координаты одного нижнего угла двери (для каждой двери);
- окна: высота, ширина и координаты одного угла окна (для каждого окна);
- горючая нагрузка: координаты границ открытой поверхности;
- система пожаротушения: координаты мест расположения и размеры отверстий для подачи огнетушащего вещества (спринклеры, дренчеры и т.д.);
- система дымоудаления: координаты мест расположения и размеры дымовых люков и дымовых клапанов;
- система механической вентиляции: координаты мест расположения и размеры отверстий в приточных и вытяжных коробах.
4.1.5. Из анализа объемно-планировочных решений, назначения и характеристик помещения, а также размещения, вида и количества типовой горючей нагрузки находятся следующие теплофизические и химические свойства (по типовой базе горючей нагрузки [5.17], Приложение 5 к настоящим Рекомендациям), а также другие характеристики горючей нагрузки:
- низшая рабочая теплота сгорания;
- удельная скорость выгорания;
- потребление кислорода при горении;
- удельное дымовыделение;
- удельное выделение окиси углерода;
- удельное выделение двуокиси углерода;
- скорость распространения пламени (в случае твердого горючего материала);
- время стабилизации горения (в случае горючей жидкости);
- суммарная масса горючей нагрузки.
В случаях, когда горючая нагрузка не является типовой (в помещении находится одновременно несколько различных видов горючих веществ или горючее вещество, не включенное в типовую базу [5.17]) необходимо обязательное согласование характеристик эквивалентной пожарной нагрузки [5.17] с органами государственного пожарного надзора.
4.1.6. По проектно-конструкторской документации определяется устройство строительных конструкций. Для каждой рассматриваемой конструкции находятся:
- число слоев различных материалов;
- толщина каждого слоя;
- теплофизические свойства материалов слоев конструкций по справочнику [5.23] или по Приложению 6 к настоящим Рекомендациям: плотность, удельная массовая теплоемкость, коэффициент теплопроводности и степень черноты поверхности (для внутреннего и наружного слоев) (Приложение 7 к настоящим Рекомендациям).
Величины параметров задаются в виде зависимостей от температуры или при отсутствии таких формул осредненными значениями.
4.1.7. Определяются критические температуры конструкций по Пособию [5.14] и справочной литературе [5.24].
4.1.8. Задаются начальные и граничные условия:
- температура газовой среды помещения перед пожаром;
- температура наружного воздуха;
- давление в газовой среде помещения перед пожаром;
- давление в наружном воздухе на уровне пола помещения;
- массовый расход подачи огнетушащего вещества и температура огнетушащего вещества;
- массовый расход системы дымоудаления;
- массовый расход системы механической вентиляции.
4.1.9. Выбор сценариев пожара заключается в определении наиболее неблагоприятного варианта его развития, при котором необходимое время эвакуации людей из помещений стоянки легковых автомобилей является минимальным, а прогрев строительных конструкций помещений стоянки легковых автомобилей является наиболее интенсивным. Например, при нахождении фактических пределов огнестойкости несущих конструкций различного исполнения в помещении необходимо выбрать различные сценарии, в каждом из которых нагрев одной из конструкций будет максимальным (источник возникновения горения находится поочередно вблизи каждой несущей конструкции).
4.1.10. Для проведения оптимизационных расчетов задаются различные возможные варианты параметров систем пожаротушения, дымоудаления и механической вентиляции:
- массовые расходы и координаты устройств для подачи огнетушащего вещества;
- массовые расходы и координаты отверстий (дымовых люков и дымовых клапанов) системы дымоудаления;
- массовые расходы и координаты отверстий системы механической вентиляции.
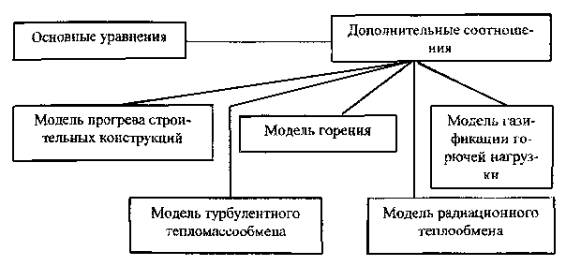
4.1.11. Выбор математических моделей для дополнительных соотношений (рис. П.1), необходимых при замыкании основной системы уравнений (П.1 + П.14) математической модели, производится в соответствии с Приложением 3 к настоящим Рекомендациям или на основе данных технической литературы [5.16, 5.18, 5.20].
4.1.12. Метод численного решения модели принимается по Приложению 4 к настоящим Рекомендациям или выбирается на основе данных технической литературы [5.25, 5.26].
4.1.13. С учетом конкретной геометрии задачи создаются неравномерные трехмерные конечно-разностные сетки внутри объемов помещения и несущих и ограждающих конструкций.
4.1.14. Решается замкнутая система алгебраических уравнений в соответствии с Приложением 4 к настоящим Рекомендациям. Последовательность решения системы приведена в п. П.4.9 Приложения 4. Шаг по времени определяется по формуле (П.51) того же Приложения.
4.1.15. Расчет тепломассообмена при пожаре в помещении и прогрева конструкций по разработанной модели проводится на ЭВМ.
Расчет производится из условий достижения одной из ниже перечисленных ситуаций:
- достижение строительной конструкцией предельного состояния по огнестойкости (потеря несущей способности, потеря теплоизолирующей способности или потеря целостности);
- полное выгорание горючей нагрузки;
- недостаток кислорода, при котором прекращается горение.
4.1.16. Анализ результатов расчета трехмерных полей температур внутри помещений, несущих и ограждающих конструкций, массовых концентраций кислорода и токсичных компонентов (окись и двуокись углерода), а также величин дальности видимости внутри помещений в различные моменты времени проводится с целью определения:
- необходимого времени эвакуации людей из помещений в данном случае стоянки легковых автомобилей;
- промежутка времени от начала пожара до достижения критического значения температуры (по потере несущей способности, целостности или теплоизолирующей способности в зависимости от назначения и вида конструкции) хотя бы в одном месте строительных конструкций в данном случае стоянки легковых автомобилей.
4.1.17. Фактические пределы огнестойкости строительных конструкций по потере несущей способности, потере теплоизолирующей способности и потере целостности определяются соответствующими величинами времени, полученными из расчета по данной методике и умножаемыми на коэффициент безопасности k = 0,5 ¸ 0,8 [5.27].
Коэффициент безопасности учитывает влияние срока эксплуатации конструкций, изменение горючей нагрузки, а также перепрофилирование объектов на прочностные свойства конструкций. Величина этого коэффициента определяется для каждого конкретного объекта отдельно и должна быть согласована с органами государственного пожарного надзора.
4.1.18. За оптимальный вариант параметров систем пожаротушения, дымоудаления и механической вентиляции принимается тот, который обеспечивает основные требования пожарной безопасности в данном случае к стоянкам легковых автомобилей:
- условие безопасной эвакуации людей (соответствие или превышение величины нормативного фактического времени эвакуации людей (ГОСТ 12.1.004-91) величиной необходимого времени эвакуации);
- соответствие или превышение величин фактических пределов огнестойкости несущих и ограждающих конструкций требуемых нормативных значений (СНиП 21-01-97).
4.2. Моделирование действий систем пожаротушения
4.2.1. Действие систем пожаротушения задается граничными условиями по поверхностям отверстий, через которые огнетушащее вещество подается в помещение.
В качестве геометрических условий задаются координаты граничных поверхностей отверстий, через которые огнетушащее вещество подается в помещение.
4.2.2. При тушении инертным газом (в том числе водяным паром) на поверхностях отверстий, через которые газ подается в помещение, задается проекция скорости на ось, перпендикулярную поверхности отверстия:
wпт = Gиг/(ρиг · Fпт), (1)
где: Gиг - массовый расход подачи инертного газа, кг/с;
ρиг - плотность инертного газа, кг/м3;
Fпт - площадь поверхности отверстия, м2.
Для определения локальных концентраций инертного газа (азота) в объеме помещения решается уравнение 8 табл. П.1 Приложения 3 к настоящим Рекомендациям.
Условием прекращения горения является достижение внутри области горения огнетушащей концентрации инертного газа. Величины огнетушащих концентраций для различных газообразных огнетушащих веществ приведены в [5.42] и в Приложении 8 к настоящим Рекомендациям.
4.2.3. При тушении водой в плоскости отверстий, через которые вода подается в помещение, задается проекция скорости на ось, перпендикулярную поверхности отверстия:
wпт = Gв/(ρв · Fпт), (2)
где: Gв - массовый расход подачи воды, кг/с;
ρв - плотность воды, кг/м3.
Для определения локальных концентраций воды в объеме помещения решается уравнение 9 табл. П.1 Приложения 3 к настоящим Рекомендациям. Учет фазовых превращений (испарение воды и конденсация водяного пара) осуществляется в источниковом члене mH2O, методы расчета которого приведены в [5.33], или в граничных условиях на поверхностях конструкций.
Источниковый член в случае испарения воды имеет вид:
![]() (3)
(3)
где: α - коэффициент теплоотдачи от капли жидкости к газовой среде, Вт/(м2 · К);
Т - температура газовой среды, К;
Тж - температура капли жидкости, К;
Тк - температура кипения, К;
cрг, срж - удельные массовые теплоемкости газовой и жидкой фазы соответственно, Дж/(кг · К);
r - удельная теплота парообразования, Дж/кг;
Fк - площадь поверхности капни жидкости, м2;
Nк - числовая плотность капель жидкости в единице объема среды, 1/м3.
Граничные условия при конденсации пара на поверхностях конструкций определяются по следующей формуле:
![]() (4)
(4)
где: j - массовая скорость конденсации, кг/(с · м2);
q - плотность теплового потока в поверхность конструкции, Вт/(м2 · К);
Tгр - температура поверхности конструкции, К.
4.3. Моделирование действий систем механической вентиляции и дымоудаления
4.3.1. Действие систем механической вентиляции и дымоудаления задается граничными условиями по плоскостям вентиляционных отверстий и люков дымоудаления.
В качестве геометрических условий задаются координаты граничных плоскостей вентиляционных отверстий и люков (клапанов) дымоудаления.
4.3.2. В плоскости вентиляционных отверстий вытяжной механической вентиляции задается проекция скорости на ось, перпендикулярную плоскости отверстия:
wвыт = Wвыт/Fвыт, (5)
где: Wвыт - объемная производительность вытяжной вентиляции, м3/с;
Fвыт - площадь поверхности вентиляционного отверстия, м2.
4.3.3. В плоскости вентиляционных отверстий приточной механической вентиляции задается проекция скорости на ось, перпендикулярную плоскости отверстия:
wпр = Wпр/Fпр, (6)
где: Wпр - объемная производительность приточной вентиляции, м3/с;
Fпр - площадь вентиляционного отверстия, м2.
4.3.4. В плоскости отверстий системы дымоудаления задается проекция скорости на ось, перпендикулярную плоскости отверстия:
wд = Wд/Fд, (7)
где: Wд - объемная производительность системы дымоудаления, м3/с;
Fд - площадь отверстия, через которое удаляется дым, м2.
4.4. Рекомендации по проведению расчетов
4.4.1. Представленная методика расчета необходимого времени эвакуации людей и фактических пределов огнестойкости строительных конструкций для оптимизации действий систем пожаротушения, дымоудаления и механической вентиляции может быть реализована на практике только на основе разработки компьютерной программы или приобретения существующих программных пакетов (например, SOFIE [5.28], PHOENICS [5.29], FLUENT [5.30] и др.).
4.4.2. Выбор математических моделей, входящих в настоящую методику, является одним из возможных вариантов расчета. В зависимости от особенностей конкретного объекта возможно применение других моделей, используемых в проектной практике.
4.4.3. Для корректного проведения расчетов по данной методике для конкретного объекта необходимо согласование с органами пожарной охраны характеристик нетиповой горючей нагрузки (п. 4.1.5 настоящих Рекомендаций) и величины коэффициента, учитывающего влияние срока эксплуатации конструкций, изменения горючей нагрузки, а также перепрофилирование объектов на прочностные свойства конструкций (п. 4.1.17 настоящих Рекомендаций).
4.4.4. Сравнительными ориентирами по величинам необходимого времени эвакуации людей и фактических пределов огнестойкости строительных конструкций при проведении расчетов по данной методике могут служить данные, приведенные в ГОСТ 12.1.004-91, Пособии [5.14] и технической литературе [5.24, 5.31].
5. ССЫЛКИ НА НОРМАТИВНО-МЕТОДИЧЕСКИЕ ДОКУМЕНТЫ И ТЕХНИЧЕСКУЮ ЛИТЕРАТУРУ
5.1. Федеральный закон «О техническом регулировании» (собрание законодательства Российской Федерации, 2002, № 52 (ч. 1), ст. 5140).
5.2. СНиП 2.04.05-91*. Отопление, вентиляция и кондиционирование.
5.3. СНиП 2.04.09-84. Пожарная автоматика зданий и сооружений.
5.4. СНиП 21-01-97. Пожарная безопасность зданий и сооружений.
5.5. СНиП 2.08.02-89. Общественные здания и сооружения.
5.6. СНиП 21-02-99. Стоянки автомобилей.
5.7. МГСН 5.01-01. Стоянки легковых автомобилей.
5.8. МГСН 4.04-94. Многофункциональные здания и комплексы.
5.9. МГСН 2.07-97. Основания, фундаменты и подземные сооружения.
5.10. ГОСТ 12.1.004-91 ССБТ. Пожарная безопасность. Общие требования.
5.11. ГОСТ Р 12.3.047-98. Пожарная безопасность технологических процессов. Общие требования. Методы контроля.
5.12. ГОСТ 12.1.033-81 ССБТ. Пожарная безопасность. Термины и определения. - М.: Госстандарт России, 1981.
5.13. СТ СЭВ 383-87. Пожарная безопасность в строительстве. Термины и определения.
5.14. «Пособие по определению пределов огнестойкости конструкций, пределов распространения огня по конструкциям и групп возгораемости материалов (к СНиП II-2-80)». М., 1985.
5.15. Дополнение № 1 к МГСН 5.01-01. Стоянки легковых автомобилей.
5.16. A.M. Рыжов, И.Р. Хасанов, А В. Карпов и др. Применение полевого метода математического моделирования пожаров в помещениях. Методические рекомендации. М. ВНИИПО, 2003.
5.18. С.В. Пузач Математическое моделирование газодинамики и тепломассообмена при решении задач пожаровзрывобезопасности. М., Академия ГПС МЧС России, 2003.
5.19. В.Л. Гинзбург Какие проблемы физики и астрофизики представляются сейчас особенно важными и интересными (тридцать лет спустя, причем уже на пороге XXI века)? // Успехи физических наук, 1999. Т. 169, № 4.
5.20. В.М. Астапенко, Ю.А. Кошмаров, И.С. Молчадский, А.Н. Шевляков Термогазодинамика пожаров в помещениях. М., Стройиздат, 1986.
5.21. А.Н. Баратов Горение - Пожар - Взрыв - Безопасность. М., ФГУ ВНИИ ПО МЧС России, 2003.
5.22. Ю.А. Кошмаров Прогнозирование опасных факторов пожара в помещении: Учебное пособие. М., Академия ГПС МВД России, 2000.
5.24. И.Л. Мосалков, Г.Ф. Плюсника, А.Ю. Фролов Огнестойкость строительных конструкций. М., Спецтехника, 2001.
5.25. Л.Г. Лойцянский Механика жидкости и газа. М., Наука, 1987.
5.26. С. Патанкар Численные методы решения задач теплообмена и динамики жидкости. М., Энергоатомиздат, 1984.
5.27. П.Н. Марчук, В.И. Присадков, В.В. Лицкевич, В.Н. Пятков, А.В. Федориков Пожарная безопасность автостоянок // Пожарная безопасность. 2003. № 6.
5.28. Welch S., Rubini P. SOFIE: Simulation of Fires in Enclosures. User Guide. United Kingdom: Cranfield University. - 1996. - 340 p.
5.29. Spalding D.B. Older and newer approaches to the numerical modelling of turbulent combustion // 3-rd International Conference on Computers in Reciprocating Engines and Gas Turbines. London: IMochE, 1996.
5.30. FLUENT 5. Tutorial Guide. V.I. Lebanon. USA. Fluent Inc. 1998.
5.31. А.И. Яковлев Расчет огнестойкости строительных конструкций. М., Стройиздат, 1988.
5.32. А.Я. Базилевич, СВ. Пузач, Д.Г. Карпенко, Е.С. Пузач, Е.В. Сулейкин Особенности разработки противопожарных мероприятий при строительстве зданий многофункционального назначения со сложной геометрией // Пожаровзрывобезопасность. 2004. № 1.
5.33. С.С. Кутателадзе Основы теории теплообмена. М., Атомиздат, 1979.
5.34. Л.В. Гурвич, И.В. Вейц, В.А. Медведев и др. Термодинамические свойства индивидуальных веществ. Справочное издание в 4-х т. М., Наука, 1982.
5.35. М.П. Вукалович, И.И. Новиков Техническая термодинамика М., Энергия, 1968.
5.37. М.Н. Оцисик Сложный теплообмен. М., Мир, 1976.
5.38. B.F. Magnussen, H.B. Hjertager. On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. 16* Sump. (Int.) Combust. The Combustion Institute. Pittsburg, 1976.
5.39. Д. Драйздейл Введение в динамику пожаров. М., Стройиздат, 1988.
5.40. Э.П. Волков, Л.И. Зайчик, В.А. Першуков Моделирование горения твердого топлива. М., Наука, 1994.
5.42. Пожаровзрывоопасность веществ и материалов и средства их тушения / А.Н. Баратов, А.Я. Корольченко, Г.Н. Кравчук и др. М., Химия, 1990.
5.43. Н.И. Зенков Строительные материалы и поведение их в условиях пожара. М, ВИПТШ МВД СССР, 1974.
5.44. Ю.А. Кошмаров и др. Лабораторные работы по курсу «Термодинамика и теплопередача в пожарном деле». М., ВИПТШ МВД СССР, 1983.
5.45. М.Я. Ройтман Пожарная профилактика в строительном деле. М., ВИПТШ МВД СССР, 1975.
5.46. М.П. Башкирцев, А.Я. Волошук, В.Г. Лимонов, В.И. Поповский Задачник по термодинамике и теплопередаче в пожарном деле. М, ВИПТШ МВД СССР, 1979.
5.47. В.Н. Демяхин, И.Л. Мосалков, Г.Ф. Плюснина, Б.Б. Серков, А.Ю. Фролов, Е.Т. Шурин Здания, сооружения и их устойчивость при пожаре. М., Академия ГПС МЧС России, 2003.
5.48 С.В. Пузач, А.П. Чумаченко, Ю.И. Козлов, В.М. Бубнов, B.C. Родин Методика расчета с компьютерной программой по определению фактических пределов огнестойкости и моделирования действий систем пожаротушения, механической вентиляции и дымоудаления при пожарах. М, ВДПО. 2004.
ПРИЛОЖЕНИЯ
Приложение 1.
Термины и определения
|
|
Термин |
Определение |
|
1 |
2 |
3 |
|
1 |
Время стабилизации горения горючей жидкости |
Промежуток времени от начала горения до выхода на режим горения с постоянной скоростью выгорания |
|
2 |
Горение взрывное |
Горение при скорости распространения пламени, большей ≈10 м/с и меньшей ≈103 м/с |
|
3 |
Горение детонационное |
Горение при скорости распространения пламени, большей ≈103 м/с |
|
4 |
Горение дефлаграционное |
Горение при скорости распространения пламени, меньшей ≈10 м/с |
|
5 |
Граничные условия |
Условия тепломассообмена на граничных поверхностях расчетной области |
|
6 |
Диффузия |
Самопроизвольный процесс переноса вещества из области с большей его концентрацией в область с меньшей концентрацией |
|
7 |
Дискретный аналог дифференциального уравнения для функции Ф |
Алгебраическое уравнение, являющееся аппроксимацией дифференциального уравнения и связывающее значения функции Ф в некоторой группе узловых точек |
|
8 |
Идеальный газ |
Газ, подчиняющийся уравнению состояния Клапейрона-Менделеева |
|
9 |
Конвективный тепловой поток |
Тепловой поток, обусловленный макроскопическим (видимым) движением газа или жидкости в пространстве из области с одной температурой в область с другой температурой и теплопроводностью |
|
10 |
Конечно-разностный метод решения дифференциального уравнения |
Численный метод решения дифференциального уравнения, основанный на дискретизации области непрерывного изменения аргумента (координаты и время) и создании и решении дискретного аналога дифференциального уравнения |
|
11 |
Конечно-разностная сетка |
Совокупность узловых точек, заменяющих области непрерывного изменения аргумента (координаты и время) |
|
12 |
Конечно-разностная схема |
Множество алгебраических соотношений, связывающих значения функции Ф в нескольких соседних узлах конечно-разностной сетки |
|
13 |
Контрольный объем |
Расчетная область вокруг одного узла конечно-разностной сетки |
|
14 |
Коэффициент теплоотдачи |
Физическая величина, равная конвективному тепловому потоку, проходящему через единицу площади твердой поверхности в условиях ее обтекании газом или жидкостью при разности температур между газом (или жидкостью) и поверхностью в 1 К |
|
15 |
Лучистый (радиационный) тепловой поток |
Тепловой поток, обусловленный переносом энергии электромагнитными волнами |
|
16 |
Модель турбулентности |
Математическая модель расчета параметров турбулентного тепломассообмена |
|
17 |
Неявная конечно-разностная схема |
Конечно-разностная схема, в которой алгебраические соотношения связывают значения функции Ф в нескольких соседних узлах конечно-разностной сетки на следующем шаге по времени3 |
|
18 |
Оптическая плотность дыма |
Произведение средней концентрации твердых частиц дыма на объем и эффективное сечение экстинции (ослабления излучения) |
|
19 |
Полевая модель |
Математическая модель расчета полей параметров тепломассообмена в помещении при пожаре |
|
20 |
Степень черноты |
Отношение интенсивности собственного излучения тела к интенсивности излучения абсолютно черного тела при одинаковых условиях |
|
21 |
Тепломассообмен |
Процесс обмена энергией в форме теплоты и массой между взаимодействующими макроскопическими частями термодинамической системы |
|
22 |
Теплопроводность |
Процесс передачи энергии от более нагретых частей тела к менее нагретым частям этого тела, обусловленный хаотическим (тепловым) движением микрочастиц при условии отсутствия макроскопического (видимого) движения макроскопических частей тела друг относительно друга |
|
23 |
Турбулентная диффузия |
Перенос массы между слоями жидкости или газа за счет турбулентного пульсационного движения |
|
24 |
Турбулентная вязкость |
Перенос импульса между слоями жидкости или газа за счет турбулентного пульсационного движения |
|
25 |
Условия однозначности |
Особенности конкретной задачи тепломассообмена, состоящие из геометрических, физических, начальных и граничных условий |
Приложение 2.
Коэффициенты и постоянные физические величины, используемые в расчетах
|
№ |
Коэффициенты и постоянные физические величины |
Обозначение |
Размерность |
Значение |
|
1 |
Ускорение свободного падения |
g |
м/с2 |
9,81 |
|
2 |
Коэффициент излучения абсолютно черного тела |
σ |
Вт/(м2 · К4) |
5,67 · 10-8 |
|
3 |
Константы k-ε модели турбулентности |
C1 |
- |
1,44 |
|
C2 |
- |
1,92 |
||
|
σk |
- |
1,0 |
||
|
σε |
- |
1,3 |
||
|
Cμ |
- |
0,09 |
||
|
4 |
Массовая концентрация кислорода в атмосферном воздухе |
XO2a |
- |
0,23 |
|
5 |
Массовая концентрация азота в атмосферном воздухе |
XN2a |
- |
0,77 |
Приложение 3.
Математическая модель
П.3.1. Пожар в помещении протекает в сложных термогазодинамических условиях при одновременном воздействии ряда возмущающих течение факторов:
- неизотермичность (отличие температур твердых поверхностей несущих и ограждающих конструкций и газовых потоков);
- сжимаемость (плотность газа не является постоянной величиной);
- градиенты давления;
- вдув на стенке (поступление в помещение продуктов внутренней деструктуризации материала твердых конструкций, испарение воды, содержащейся внутри материала конструкций, тепло массообменная защита конструкций);
- излучение;
- протекание химических реакций;
- двухфазность (одновременное сосуществование нескольких фаз газ + твердые частицы, газ + жидкость, газ + твердые частицы + жидкость);
- шероховатость поверхностей несущих и ограждающих конструкций;
- кривизна поверхности несущих и ограждающих конструкций;
- турбулентность;
- скачки уплотнения;
- переход ламинарного режима течения в турбулентный.
Действие вышеуказанных факторов приводит к существенному отличию закономерностей тепломассообмена от хорошо изученных «стандартных» условий теплообмена [5.33]: изотермическое безградиентное течение несжимаемого газа вдоль поверхности непроницаемой пластины. Поэтому методы расчета тепломассообмена при пожаре должны учитывать влияние термогазодинамических условий его развития.
П.3.2. К числу основных особенностей тепло массообменных процессов при пожаре относятся следующие [5.18]:
- наибольшая разница давлений в разных зонах помещения не превышает десятых долей процента от величины среднего давления в помещении при отсутствии взрывов с образующимися ударными волнами;
- скорости потоков газов малы по сравнению со скоростью звука (при отсутствии детонационного горения и ударных волн);
- скорости диффузии газов достаточно велики, т.е. необходимо учитывать процессы термодиффузии и турбулентной диффузии.
П.3.3. При разработке полевой математической модели расчета тепломассообмена при пожаре в помещении принимаются следующие допущения и упрощения реальной термогазодинамической картины процесса [5.18]:
- существует локальное термодинамическое и химическое равновесие во всем объеме помещения, что позволяет использовать равновесное уравнение состояния;
- газовая среда является смесью идеальных газов, что дает удовлетворительное приближение в диапазонах температур и давлений, характерных при пожаре;
- локальные скорости и температуры компонентов газовой смеси и твердых (или жидких) частиц одинаковы между собой в каждой точке пространства (односкоростная и одно-температурная модель), т.е. межфазным взаимодействием (температурным скачком и «скольжением» фаз друг относительно друга) пренебрегаем;
- коагуляцией и дроблением частиц дыма пренебрегаем;
- химическая реакция горения является одноступенчатой и необратимой;
- диссоциация и ионизация среды при высоких температурах не учитывается;
- взаимным влиянием турбулентности и излучения пренебрегаем;
- пренебрегается обратным влиянием горения на скорость выгорания горючего материала, т.е. скорость выгорания горючей нагрузки рассчитывается на основе полуэмпирических зависимостей без учета текущих параметров газовой среды;
- термо- и бародиффузией пренебрегаем.
П.3.4. Газовая среда рассматривается как вязкий теплопроводный сжимаемый идеальный газ. Влияние твердых частиц дыма учитывается при определении характеристик радиационного теплопереноса внутри помещения.
П.3.5. Полевая модель расчета тепломассообмена при пожаре состоит из системы основных дифференциальных уравнений законов сохранения массы, импульса и энергии и дополнительных уравнений, необходимых для ее замыкания. Структура полевой модели приведена на рис. П.1.
П.3.6. Все составные части полевой модели взаимосвязаны друг с другом с помощью общих параметров (обратная связь). Поэтому процесс решения полевой модели носит итерационный характер.
П.3.7. Полевая модель расчета тепломассообмена при пожаре основана на уравнениях законов сохранения массы, импульса и энергии. Подробный вывод этих уравнений приведен в технической литературе [5.25]. Для определенности ось x направлена вдоль длины, ось y - ширины и ось z - высоты помещения. Центр ортогональной системы координат находится в левом нижнем углу помещения (на плане помещения). Размерности всех параметров приведены в системе СИ.
Рис. П.1. Структура полевой модели
П.3.8. Уравнение неразрывности газовой смеси является математическим выражением закона сохранения массы газовой смеси и имеет следующий вид:
где: ρ - плотность, кг/м3;
τ - время, с;
x, y, z - координатные оси вдоль длины, ширины и высоты помещения соответственно, м;
wx, wy, wz - проекции скорости на соответствующие оси, м/с.
П.3.9. В скалярном виде векторное уравнение закона сохранения импульса для смеси газов распадается на три уравнения движения вдоль координатных осей:
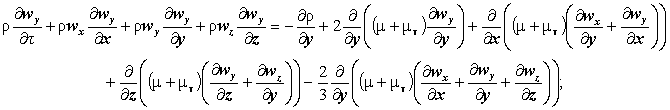 (П.3)
(П.3)
где: μ - динамический коэффициент вязкости, кг/(м · с);
μт - коэффициент турбулентной вязкости, кг/(м · с);
р - давление, Па;
ρ0 - плотность газовой среды за пределами нагретого слоя, кг/м3;
g - ускорение свободного падения, м/с2.
Уравнения (П.1 ¸ П.4) называются уравнениями Рейнольдса и получены из уравнений Навье - Стокса [5.25] путем осреднения по времени всех параметров.
П.3.10. Уравнение энергии является математическим выражением закона сохранения и превращения энергии. Для тепловых процессов (при рассматриваемых в п. П.3.1 данной методики условиях тепломассообмена при пожаре) этот закон выражается в виде первого начала термодинамики и имеет следующий вид:
где: T - температура, К;
ср - удельная изобарная теплоемкость, Дж/(кг · К);
λ - коэффициент теплопроводности, Вт/(м · К);
λт - коэффициент турбулентной теплопроводности, Вт/(м · К);
λр - коэффициент радиационной теплопроводности, Вт/(м · К):
qv - интенсивность внутренних источников тепла, Вт/м3;
qv = qvк + qvл + qvг;
где: qvл - интенсивность внутренних источников тепла за счет радиационного (лучистого) теплопереноса, Вт/м3;
qvк - интенсивность внутренних источников тепла из-за конвективного теплообмена, Вт/м3;
qvг - интенсивность внутренних источников тепла из-за реакций горения, Вт/м3.
П.3.11. Закон сохранения массы i-го газа, входящего в состав смеси, (уравнение неразрывности для компонента газовой смеси) имеет вид:
где: Xi - массовая концентрация i-го газа;
Di - коэффициент диффузии i-го газа, м2/с;
Dт - коэффициент турбулентной диффузии, м2/с;
mi - интенсивность внутренних источников (стоков) массы, возникающих из-за образования (исчезновения) молекул данного газа вследствие протекания химических реакций горения, кг/(с · м3). Величины mi определяются с учетом данных Приложения 5 к настоящим Рекомендациям по формулам, приведенным в табл. П.1.
П.3.12. Закон сохранения оптической плотности дыма используется в виде:
где: Dоп - оптическая плотность дыма, Нп/м;
qD - интенсивность внутренних источников оптической плотности дыма, образующегося из-за прохождения реакций горения, Нп/(с · м). Величина qD определяется с учетом данных Приложения 6 к настоящим Рекомендациям по формуле, приведенной в табл. П.1.
П.3.13. Уравнение состояния смеси идеальных газов имеет вид [5.35]:
p = ρRT, (П.8)
где: R - газовая постоянная смеси, Дж/(кг · К).
П.3.14. Уравнения теплофизических параметров смеси газов учитывают химический состав смеси. В состав смеси входят следующие газы: кислород, азот, продукты горения (окись углерода, двуокись углерода) и продукты горения горючей нагрузки. Газовая постоянная, плотность и удельная изобарная теплоёмкость смеси газов вычисляются по формулам:
![]()
![]()
![]() (П.9)
(П.9)
где: i - номер газовой компоненты смеси;
n - число газов в смеси;
ri, gi, Ri, cpi, ρi - объемная и массовая доля, газовая постоянная (Дж/(кг · К)), удельная изобарная массовая теплоемкость (Дж/(кг · К)) и плотность (кг/м3) i-ой компоненты газовой смеси. Величины удельных изобарных массовых теплоёмкостей компонентов принимаются постоянными или определяются в зависимости от температуры. Соответствующие зависимости приводятся в справочной литературе [5.34].
П.3.15. Таким образом, решаются нестационарные трехмерные дифференциальные уравнения в частных производных законов сохранения массы, импульса и энергии для газовой среды помещения, уравнения сохранения массы для компонентов газовой среды и уравнение оптической плотности дыма. Все дифференциальные уравнения приведены к «стандартному» виду [5.26], удобному для численного решения:
где: Ф - зависимая переменная (энтальпии газовой смеси и материала стен и перекрытия, проекции скорости на координатные оси, концентрации компонентов газовой смеси, кинетическая энергия турбулентности и скорость ее диссипации, массовая концентрация и оптическая плотность дыма);
Г - коэффициент диффузии для Ф;
S - источниковый член для Ф.
П.3.16. Значения величин в уравнении (П.10) приведены в табл. П.1. Все величины здесь и далее являются осредненными по времени. При расчете прогрева ограждающих конструкций (уравнения 11 и 12, табл. П.1): wx = wf = wz = 0.
Обозначения в табл. П.1 следующие:
XO2, XCO, XCO2, XN2, XH2O, Xпг - массовые концентрации кислорода, продуктов горения (окиси углерода и двуокиси углерода), азота, воды и продуктов горения горючей нагрузки;
DO2, DCO, DCO2, DN2, DH2O, Dпг - коэффициенты диффузии кислорода, окиси углерода, двуокиси углерода, азота, воды и продуктов горения горючей нагрузки, м2/с;
mO2, mCO, mCO2 - интенсивность внутренних стоков массы кислорода и источников массы окиси углерода и двуокиси углерода, возникающих из-за образования (исчезновения) молекул данного газа вследствие Протекания химических реакций горения, кг/(с · м3);
mH2O - интенсивность внутренних источников (стоков) массы воды (водяного пара), возникающих из-за испарения воды (конденсации водяного пара) под влиянием поля температур в помещении и в ограждающих конструкциях, кг/(с · м3);
β = 1/T - коэффициент объемного термического расширения, 1/К;
LO2 - потребление по массе кислорода при сгорании 1 кг горючего материала;
LCO, LCO2 - выделение по массе окиси и двуокиси углерода при сгорании 1 кг горючего материала;
Ψг - скорость выгорания горючего материала, кг/с;
Dопг - дымообразующая способность горючего материала, Нп · м2/кг;
i, iw, ic - энтальпии газовой смеси, материала стен и перекрытия, Дж/кг;
Qри - низшая рабочая теплота сгорания, Дж/кг;
η - полнота сгорания;
qD - интенсивность внутренних источников оптической плотности дыма, образующегося из-за протекания реакций горения, Нп/(с · м);
qvw, qvc - интенсивность внутренних источников теплоты внутри стен и перекрытия, Вт/м3;
ΔV - объем газовой среды, внутри которой находится источник (сток) массы или энергии, м3.
Таблица П.1
Параметры и коэффициенты уравнения (П.10)
|
Ф |
Г |
S |
|
|
1 |
1 |
0 |
0 |
|
2 |
wх |
μ + μт |
|
|
3 |
wy |
μ + μт |
|
|
4 |
wz |
μ + μт |
|
|
5 |
XO2 |
(DO2 + Dт)ρ |
mO2 = LO2Ψгη/ΔV |
|
6 |
XCO |
(DCO + Dт)ρ |
mCO = LCOΨгη/ΔV |
|
7 |
XCO2 |
(DCO2 + Dт)ρ |
mCO2 = LCO2Ψгη/ΔV |
|
8 |
XN2 |
(DN2 + Dт)ρ |
0 |
|
9 |
XH2O |
(DH2O + Dт)ρ |
mH2O |
|
10 |
Xпг |
(Dпг + Dт)ρ |
mпг |
|
11 |
Dоп |
0 |
qD = DопгΨг/ΔV |
|
12 |
iw |
λw |
qvw |
|
13 |
ic |
λc |
qvc |
|
14 |
i |
λ + λт + λл |
ΨгηQри/ΔV - qvp |
П.3.17. Уравнение теплопроводности является математически выражением закона сохранения и превращения энергии. Проводится отдельный расчет температурных полей в стенах, полу и перекрытии с использованием нестационарных трехмерных дифференциальных уравнений теплопроводности в следующем виде [5.36]:
![]() (П.12)
(П.12)
где: Тw, Тf, Тс - локальные температуры материалов стен, пола и перекрытия соответственно, К;
ρw, ρf, ρс - плотности материалов стен, пола и перекрытия, кг/м3;
cw, cf, cc - удельные теплоемкости материалов стен, пола и перекрытия, Дж/(кг · К);
λw, λf, λс - коэффициенты теплопроводности материалов стен, пола и перекрытия, Вт/(м · К);
qvw, qvf, qvс - интенсивность внутренних источников теплоты, Вт/м3.
При отсутствии фазовых переходов внутри материалов конструкций qvw = qvf = qvс = 0. Для случаев фазовых превращений методы расчета интенсивности внутренних источников теплоты приводятся в технической литературе [5.25].
П.3.18. Для колонны с прямоугольной формой поперечного сечения решается уравнение (П.11), в котором величины плотности, удельной теплоемкости и коэффициента теплопроводности соответствуют материалу колонны.
В случае с круглой формой поперечного сечения решается уравнение теплопроводности, записанное в цилиндрической системе координат [5.36]:
где Тk - локальная температура материала колонны, К;
ρk, ck и λk - плотность (кг/м3), удельная теплоемкость (Дж/(кг · К)) и коэффициент теплопроводности (Вт/(м · К)) материала колонны;
r - координата вдоль радиуса колонны, м;
θ - угловая координата, рад;
zk - координата вдоль высоты колонны, м;
qvk - интенсивность внутренних источников теплоты, Вт/м3.
При отсутствии фазовых переходов внутри материала колонны qvk = 0.
П.3.19. При произвольной форме сечений строительных конструкций решается уравнение (П.11). При этом необходимо, чтобы координатные оси были согласованы с формой контуров конструкции, и при численном решении дифференциального уравнения необходима генерация ортогональной конечно-разностной сетки.
П.3.20. Начальные условия к уравнениям (П.11 ¸ П.13) принимаются следующие:
- если температура газовой среды внутри помещения равна температуре наружного воздуха, то Tw0 = Tc0 = Tf0 = Tα;
- если температуры внутри и снаружи помещения не равны, то распределение температур по толщине конструкций принимается кусочно-линейным (в пределах каждого слоя) от температуры на внутренней поверхности, равной Tm0, до температуры наружной поверхности, равной Tα, из решения стационарной одномерной задачи теплопроводности через плоскую стенку с граничными условиями первого рода [5.36].
Здесь Tw0, Tc0, Tf0 и Tm0 - соответственно начальные (перед пожаром) температуры стен, перекрытия, пола и воздуха в помещении.
Начальные условия к уравнению (П.14) имеют вид: температура материала колонны равна начальной температуре воздуха в помещении Tk0 = Tm0.
П.3.21. Граничные условия к уравнениям (П.11 ¸ П.14) на внутренних поверхностях негорючих конструкций являются сложными граничными условиями [5.33] и имеют следующий вид:
q1 = qк + qл, (П.15)
где: q1 - локальная плотность суммарного теплового потока в конструкцию, Вт/м;
qк - локальная плотность конвективного теплового потока в конструкцию, Вт/м2;
qл - локальная плотность лучистого теплового потока в конструкцию, Вт/м2.
Локальные плотности лучистых тепловых потоков, поступающих в конструкцию, определяются в соответствии с математической моделью, приведенной в пунктах П.3.39 ¸ П.3.42 данного Приложения, локальные плотности конвективных тепловых потоков - в пунктах П.3.28 ¸ П.3.35.
Значения степени черноты внутренней поверхности ряда строительных конструкций приведены в Приложении 7 к настоящим Рекомендациям.
П.3.22. Граничные условия к уравнениям (П.11 ¸ П.14) на наружных поверхностях негорючих конструкций являются сложными граничными условиями [5.36] и имеют следующий вид:
q2 = ε2σ(T24 - Ta4) + α2(T2 - Ta), (П.16)
где q2 - локальная плотность суммарного теплового потока от конструкции к окружающей среде, Вт/м2;
T2 - локальная температура наружной поверхности конструкции, К;
Ta - температура окружающего воздуха, К;
ε2 - степень черноты наружной поверхности конструкции;
σ - коэффициент излучения абсолютно черного тела, Вт/(м · К4);
α2 - локальный коэффициент теплоотдачи при свободной конвекции на наружных поверхностях конструкции в окружающую среду, Вт/(м2 · К).
Значения степени черноты наружной поверхности ряда строительных конструкций приведены в Приложении 7 к настоящим Рекомендациям.
Величина локального коэффициента теплоотдачи определятся по формулам свободной конвекции [5.36] (из зависимостей Nu = C(GrPr)m,
где: Nu - число Нуссельта;
Gr - число Грасгофа;
Pr - число Прандтля;
константы C и m определяются в зависимости от расположения поверхности и произведения Gr · Pr; торцовые поверхности считаются теплоизолированными).
П.3.23. Сопряжение расчета теплового состояния ограждающих конструкций помещения с полевой математической моделью пожара производится через величину теплового потока, отводимого из помещения в ограждающие конструкции.
П.3.24. В случае многослойных конструкций, когда слои выполнены из различных материалов, предполагается идеальный тепловой контакт на границах между соседними слоями.
П.3.25. Локальные величины плотности, удельной теплоемкости и коэффициента теплопроводности материалов отдельных слоев в общем случае зависят от локальной температуры и влажности. Соответствующие значения вышеперечисленных теплофизических параметров приводятся в справочной литературе [5.23] и представлены в Приложении 6 к настоящим Рекомендациям.
П.3.26. Дифференциальные уравнения теплопроводности в частных производных (П.11 ¸ П.13) могут быть приведены к стандартному виду (П.10) (см. уравнения 12 и 13, табл. П.1 данного Приложения).
П.3.27. Приведенная в данном параграфе математическая модель расчета теплового состояния материалов стен, перекрытия, пола и колонны применима для определения температуры конструкции с сечением любой формы.
П.3.28. В турбулентных потоках газовой среды при пожаре скорость, давление, температура и другие параметры испытывают беспорядочные колебания (пульсации). Мгновенное распределение всех величин в любой момент времени в помещении с заданными геометрическими параметрами не определяется однозначно только системой исходных уравнений и начальными и граничными условиями, но также существенно зависит от малых случайных возмущений (из-за неустойчивости движения).
Известные модели турбулентности k-ε, k-ω, алгебраические и другие [5.25, 5.26] показывают, что каждому конкретному случаю течения соответствует вполне определенный набор констант модели. В любой модели турбулентности оговорен круг течений и условий, для которых она справедлива. Особую сложность представляет собой выбор модели при учете сложных граничных условий, обусловленных тепломассообменной защитой стенок конструкций, например, при защите оборудования от теплового воздействия пожара. Константы моделирования еще недостаточно систематизированы для широкого круга даже стационарных безотрывных течений.
Таким образом, математическое моделирование турбулентного конвективного тепломассообмена при пожаре требует тщательного выбора модели турбулентности для конкретных условий пожара.
П.3.29. Наиболее разработанной и часто используемой для расчета тепломассообмена при пожаре является градиентная модель турбулентности - k-ε модель [5.25]. В этой модели предполагается, что коэффициент турбулентной вязкости зависит от кинетической энергии турбулентности и скорости ее диссипации в соответствии с формулой Колмогорова [5.25]:
где: v, vт - кинематический коэффициент молекулярной и турбулентной вязкости соответственно, м2/с;
![]() - кинетическая
энергия турбулентности, м2/с2;
- кинетическая
энергия турбулентности, м2/с2;
w'х, w'y, w'z - пульсационные составляющие проекций скорости на соответствующие оси, м/с;
Сμ = 0,09 - эмпирическая константа;
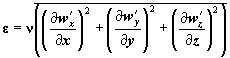 - скорость диссипации
кинетической энергии турбулентности, м2/с3.
- скорость диссипации
кинетической энергии турбулентности, м2/с3.
П.3.30. Коэффициент молекулярной динамической вязкости газа определяется по величине кинематической молекулярной вязкости, вычисляемой по формуле Сезерленда [5.33]:
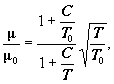
где: С - эмпирическая константа для конкретного газа, К;
μ - коэффициент молекулярной динамической вязкости, кг/(м · с);
μ0 - известная величина динамической вязкости при выбранной температуре Т0, кг/(м · с). Величины С и Т0 находятся из справочной литературы [5.33].
П.3.31. Для нахождения кинетической энергии турбулентности и скорости ее диссипации решаются следующие дифференциальные уравнения законов сохранения соответствующих величин [5.25]:
В стандартной k-ε модели турбулентности набор эмпирических констант является следующим [5.19]: C1 = 1,44; С2 = 1,92; σk = 1,0; σε = 1,3; Сμ = 0,09. В области конвективной колонки модель модернизируется: C1 = l,6.
П.3.32. Для определения коэффициентов турбулентной теплопроводности смеси λт (уравнение энергии (П.5)) и турбулентной диффузии компонентов Dт (уравнения неразрывности для газовых компонентов (П.6)) используется тройная аналогия Прандтля [5.33]: при равенстве чисел Прандтля и Льюиса единице (Pr = Le = 1) и отсутствии градиента давления в потоке газа (dp/dx = 0, dp/dy = 0, dp/dz = 0) уравнения движения (П.2 ¸ П.4), энергии (П.5) и диффузии (П.6) становятся тождественными и в случае подобия граничных условий существует подобие полей скоростей, температур и концентраций.
Турбулентное и диффузионное числа Прандтля принимаем равными Prт = Prд = 1. Тогда коэффициент турбулентной теплопроводности определяется из соотношения:
![]() (П.21)
(П.21)
а коэффициент турбулентной диффузии равен:
Dт = μт/ρPrд. (П.22)
Молекулярная теплопроводность равна [5.33] (при Pr = const и слабой зависимости удельной теплоемкости от температуры):
![]()
где: λ0 - известная величина коэффициента теплопроводности при выбранной температуре T0, Вт/(м · К).
П.3.33. Уравнения (П.17 ¸ П.23) позволяют определить коэффициенты турбулентной вязкости, теплопроводности и диффузии, входящие в уравнения полевой модели (П.2 ¸ П.6).
П.3.34. Граничные условия к уравнениям (П.19) и (П.20) имеют вид:
- на твердой негорючей поверхности:
дk/дn = 0; (П.24)
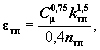 (П.25)
(П.25)
где: kтп - величина кинетической энергии турбулентности в ближайшем к поверхности узле конечно-разностной сетки, м2/с2;
εтп - величина скорости диссипации кинетической энергии турбулентности в ближайшем к поверхности узле конечно-разностной сетки м2/с3;
nтп - расстояние по нормали n от твердой поверхности до ближайшего к поверхности узла конечно-разностной сетки, м;
- в плоскости поперечного сечения открытых проемов:
дk/дn = 0; дε/дn = 0;, (П.26)
где: n - направление по нормали к плоскости открытого проема.
П.3.35. Уравнения (П.19) и (П.20) могут быть приведены к стандартному виду (П.10).
П.3.36. Для расчета лучистого теплообмена в излучающем, поглощающем и рассеивающем газе записывается дополнительное интегро-дифференциальное уравнение для переноса лучистой энергии в газовой среде, которое решается различными методами в зависимости от конкретных условий задачи. Уравнение имеет вид [5.37]:
где: αλ, βλ - спектральные коэффициенты поглощения и рассеяния излучения, 1/м;
γλ(s,s') - спектральная индикатриса рассеяния;
ω' - телесный угол в направлении s', рад;
Iλ(x,s), Iλ0(x,s) - спектральная интенсивность излучения в точке х в направлении s данного и абсолютно черного тела, Вт/м2.
П.3.37. Уравнение переноса излучения (П.27) может быть решено достаточно точными и универсальными численными способами, например, зональным методом или стохастическим методом Монте-Карло [5.37]. Однако, эти методы не вполне совместимы с сеточными методами решения уравнений переноса импульса и энергии полевой термогазодинамики пожара, что требует разных численных алгоритмов и приводит к существенному усложнению программного комплекса. Кроме того, спектральные характеристики излучения внутри газовой среды помещения при пожаре недостаточно изучены. Поэтому используют различные приближенные методы решения уравнения (П.27).
П.3.38. Предполагаем, что существует локальное термодинамическое равновесие внутри излучающего объема. Рассмотрим четыре приближенных математических модели расчета лучистого теплопереноса, наиболее часто используемые при моделировании пожаров [5.37]:
- оптически прозрачный неизлучающий газ;
- оптически толстый слой;
- оптически тонкий слой;
- диффузионный метод (метод моментов).
П.3.39. При использовании приближения оптически прозрачного неизлучающего газа в уравнении энергии (П.5) принимаем:
- коэффициент радиационной теплопроводности равен λл = 0;
- источниковый член qvл = 0.
П.3.40. В случае оптически толстого слоя (оптическая толщина τ0 >> 1, т.е. средняя длина свободного пробега фотона мала по сравнению с характерным размером среды) qvл = 0, а коэффициент лучистой теплопроводности равен:
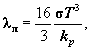 (П.28)
(П.28)
где: kp - интегральный коэффициент ослабления излучения, 1/м;
T - локальная температура слоя, К;
σ - коэффициент излучения абсолютно черного тела, Вт/(м2 · К4).
Для гетерогенной среды при этом необходимо проводить расчет
образования, движения и коагуляции твердых частиц дыма для определения их
размеров и концентрации, определяющих главным образом излучательную, поглощательную и пропускательную способности
среды. При этом коэффициент ослабления определяется как ![]()
где: dp - средний диаметр частиц дыма, м;
n - объемная концентрация частиц, 1/м3.
П.3.41. Для оптически тонкого слоя (τ0 << 1) принимается, что λл = 0, а источниковый член уравнения энергии определяется как:
qvл = 4πεpσT4, (П.29)
где: εp - интегральная степень черноты газа.
П.3.42. При промежуточной величине оптической толщины слоя газа используется диффузионный метод (метод моментов). При этом λл = 0, а источниковый член в уравнении энергии равен:
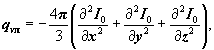 (П.30)
(П.30)
где: I0 - интенсивность излучения, определяемая из решения уравнения:
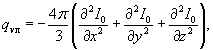
где: χp - интегральный коэффициент излучения, 1/м;
Ib(T) = σT4 - интенсивность излучения абсолютно черного тела, Вт/м2.
При выполнении закона Кирхгофа [5.33]:
εp = 1 - е-kpL, (П.32)
где: εp - интегральная степень черноты слоя газа толщиной L.
Коэффициент ослабления излучения находится по рассчитанной оптической плотности дыма (уравнение (П.7)):
kp = λ*Dоп, (П.33)
где: Dоп - локальная величина оптической плотности дыма, Нп/м;
λ* - коэффициент для пересчета оптического диапазона излучения в инфракрасный [5.18], 1/Нп.
П.3.43. При промежуточной величине оптической толщины слоя газа можно применять потоковый метод [5.16].
П.3.44. Для определения излучения только от факела в случае оптически прозрачной среды вне него степень черноты факела может быть определена следующим образом. Сначала определяется число Бугера [5.20]:
Bu = kdэкв, (П.34)
где: k - коэффициент ослабления газовой среды в объеме факела, который может быть определен по экспериментальным соотношениям работы [5.20], 1/м;
![]() - эквивалентный
диаметр поверхности горения, м;
- эквивалентный
диаметр поверхности горения, м;
Fг - площадь поверхности горючей жидкости, м2. Затем по этому значению находится степень черноты факела по экспериментальным данным работы [5.20] с учетом свойств конкретного горючего материала.
По данным работы [5.20] при числе Бугера Bu < 1 можно применять закон аддитивности, т.е. не учитывать взаимное влияние излучения и конвекции, а среду рассматривать как оптически прозрачную. Взаимное влияние конвекции и излучения проявляется при определении граничных условий на твердых поверхностях. При Bu > 1 рассматривается приближение оптически толстого слоя и учитывается влияние только излучения на характеристики турбулентности через увеличение толщины теплового пограничного слоя.
П.3.45. Для конкретных исходных данных задачи требуется Уточнение и адаптация существующих математических моделей лучистого переноса в сплошной среде с привлечением дополнительной экспериментальной информации по коэффициентам переноса при реальной термогазодинамической картине пожара.
П.3.46. Могут использоваться иные модели радиационного теплопереноса, приведенные в литературе [5.16, 5.37], например, метод дискретного радиационного переноса.
П.3.47. В случае горючей жидкости скорость выгорания горючего материала задается следующими полуэмпирическими соотношениями [5.22]:
при τ ≤ τст: ![]() (П.35)
(П.35)
при τ > τст: ![]() (П.36)
(П.36)
где: τ - время, с;
τст - время стабилизации горения, с;
Fг - площадь открытой поверхности горючей жидкости, м2;
Ψ0 - удельная скорость выгорания горючего материала, кг/(с · м2).
Время стабилизации горения и удельная скорость выгорания горючего материала определяются по справочной литературе [5.17] в зависимости от вида жидкости. Параметры процесса выгорания для ряда горючих жидкостей приведены в Приложении 5 к настоящим Рекомендациям.
П.3.48. Для твердого горючего материала скорость выгорания горючего материала определяется по формуле [5.22]:
где: Fг = πr2 - площадь открытой поверхности горючего материала, охваченная горением, м;
r = wлсτ - радиус горения, м;
wлс - линейная скорость распространения пламени по поверхности горючего материала, м/с.
Удельная скорость выгорания горючего материала определяются по справочной литературе [5.17] в зависимости от его вида. Параметры процесса выгорания для ряда твердых горючих материалов представлены в Приложении 5 к настоящим Рекомендациям.
П.3.49. В случае горючего газа задаются массовая скорость, параметры газа (давление и температура) и размеры области его натекания.
П.3.50 Для определения величины оставшейся массы жидкого или твердого горючего материала решается уравнение закона сохранения массы [5.22]:
![]() (П.38)
(П.38)
где: М - остаточная масса горючего материала.
П.3.51. В основных уравнениях полевой модели область горения (факел) моделируется внутренними источниками энергии, массы и дыма или задаются экспериментально измеренные поля температур и других параметров в этой области.
Моделирование очага горения может быть выполнено с помощью двух основных подходов:
- моделирование источниками энергии, массы и дыма без учета химической кинетики и термогазодинамических условий в области горения;
- непосредственно модели горения.
П.3.52. Среди непосредственно моделей горения можно выделить следующие:
- диффузионно-вихревая модель [5.38];
- модель ламинарных элементов пламени [5.16] и т.д.
В моделях горения, как правило, предполагают, что химическое взаимодействие в области горения протекает бесконечно быстро по сравнению с тепло массообменными процессами. Поэтому скорость протекания химических реакций горения определяется тепло массообменными процессами, т.е. скоростями доставки в зону горения и перемешивания горючего и окислителя (диффузионное горение).
П.3.53. При моделировании источниками энергии, массы и дыма без
учета химической кинетики и термогазодинамических условий в области горения
вышеперечисленные источники задаются в объеме параллелепипеда с площадью
основания, равной площади горючей нагрузки, охваченной горением, а высота
составляет hf = kfdэкв, где: ![]() - эквивалентный
диаметр поверхности горения, м; kf -
эмпирический коэффициент [5.20]
для конкретной горючей нагрузки.
- эквивалентный
диаметр поверхности горения, м; kf -
эмпирический коэффициент [5.20]
для конкретной горючей нагрузки.
Мощность тепловыделения определяется по формуле:
Qг = ηΨгQрн, (П.39)
где: Qг - мощность тепловыделения, Вт;
Qрн - низшая рабочая теплота сгорания, Дж/кг;
η - полнота сгорания.
Полнота сгорания может быть рассчитана, например, по формуле [5.20]:
η = 0,63 + 0,2XO2m + 1500XO2m6, (П.40)
где: XO2m - среднеобъемная массовая концентрация кислорода в помещении.
П.3.54. В моделях горения химическая реакция горения может приниматься одно- или многоступенчатой. При этом считается, что газовая смесь состоит из кислорода, азота, газифицированной горючей нагрузки и продуктов горения.
П.3.55. Процесс горения можно представить в виде одной одноступенчатой реакции:
F + a1O2 + a13,76N2 → а2СО2 + a3СО + а4Н2О + а5С + а13,76N2 + Qr, (П.41)
где: F - горючее вещество;
a1, а2, a3, а4, а5 - коэффициенты реакции;
Qr - теплота реакции.
Величинами масс остальных продуктов горения для наиболее распространенных видов горючих материалов пренебрегаем [5.22, 5.41]. При необходимости можно учесть дополнительные образующиеся в результате прямой реакции вещества в уравнениях (П.41) и (П.6).
Азот необходимо учитывать в реакциях горения, потому что он поглощает часть тепла, выделяемого при реакции, и входит в состав продуктов горения.
П.3.56. Влияние турбулентности на протекание химических реакций горения может быть учтено с помощью различных математических моделей, например, с помощью диффузионно-вихревой модели [5.38]. Одноступенчатую реакцию горения можно представить в более упрощенном виде [5.16]:
F + sO → (1 + s)P, (П.42)
где: F, О, Р - массы горючего, окислителя и продукта реакции;
s - коэффициент.
Тогда скорость реакции равна [5.38]:
где: Gr - массовая скорость реакции в единице объема газовой среды, кг/(с · м3);
k - кинетическая энергия турбулентности, м2/с2;
ε - скорость диссипации кинетической энергии турбулентности, м2/с3;
Xf, Хо, Хр - локальные массовые концентрации продуктов выгорания горючего вещества, кислорода и продуктов горения.
П.3.57. Могут использоваться иные модели горения, приведенные в технической литературе [5.16, 5.39, 5.40], например, трехступенчатая реакция. Однако усложнение модели горения для определения фактических пределов огнестойкости строительных конструкций не приводит к повышению точности расчетов [5.39].
П.3.58. Условия однозначности к основной системе уравнений (П.1 ¸ П.10) и дополнительных соотношений (П.11 ¸ П.43) состоят из геометрических, физических, граничных и начальных условий.
П.3.59. Геометрические условия принимаются следующими:
- координаты граничных поверхностей ограждающих конструкций помещения;
- координаты граничных поверхностей громоздких предметов, находящихся в помещении;
- координаты границ открытых и закрытых (вскрытие которых возможно под тепловым воздействием пожара) проемов;
- координаты границ открытой поверхности горючего материала или источника натекания газа.
П.3.60. Физические условия имеют вид:
- теплофизические свойства компонентов газовой среды;
- теплофизические свойства материала ограждающих конструкций;
- теплофизические и химические свойства горючего материала.
П.3.61. Граничные условия:
- на внутренних поверхностях строительных конструкций:
проекции скоростей равны нулю: wx = wу = wz = 0;
для уравнения энергии: qΣ = qл + qк,
где: qл - плотность лучистого теплового потока;
qк - плотность конвективного теплового потока;
для остальных параметров Ф (обобщенное уравнение (П.10)) принимается, что дФ/дп = 0,
где: n - нормаль к поверхности;
- на открытых проемах:
для всех параметров Ф принимается, что дФ/дп = 0 в области истечения газа наружу;
в области поступления наружного воздуха внутрь давление, температура и концентрации компонентов соответствуют параметрам атмосферного воздуха (смесь кислорода и азота);
- на наружных поверхностях ограждающих конструкций:
в соответствии с уравнением (П.16);
параметры наружного воздуха: температура, скорость и направление ветра и давление;
- на открытой поверхности горючего материала:
проекция скорости перпендикулярно поверхности горючего материала (с помощью уравнений (П.35 ¸ П.37));
плотность продуктов горения.
П.3.62. Начальные условия (в начальный момент времени перед пожаром):
- помещение заполнено неподвижной смесью (воздухом) кислорода и азота:
XО2a = 0,23; XN2a = 0,77; wx = wу = wz = 0;
- параметры газовой смеси: температура и давление (распределение по высоте);
- скорость выгорания горючего материала: Ψг = 0.
Приложение 4.
Численное решение
П.4.1. Замкнутая система уравнений приведенной в данной Методике математической модели может быть решена только численным способом. Современный уровень развития вычислительной техники и вычислительной математики позволяет разработать достаточно точные численные методы, в которых реализуются различные конечно-разностные схемы исходной системы уравнений. Применяется наиболее апробированный численный метод решения систем дифференциальных уравнений в частных производных - метод «контрольных объемов» [5.26], используемый в современных программных пакетах расчета на ПЭВМ прикладных задач газодинамики и тепломассообмена PHOENICS [5.29] и FLUENT [5.30].
П.4.2. Дифференциальные уравнения в частных производных, приведенные к «стандартному» виду (П.10), решаются конечно-разностным методом «контрольных объемов» по неявной схеме [5.26]. Для трехмерной задачи дискретный аналог уравнений имеет вид (рис. П.2):
арФр = аEФE + аWФW + аNФN + аsФs + аTФT + аBФB + b, (П.44)
где: aE = DEA(|PE|) + [|-FE,0|];
aN = DNA(|PN|) + [|-FN,0|];
aT = DTA(|PT|) + [|-FT,0|];
aW = DWA(|PW|) + [|FW,0|];
as = DsA(|Ps|) + [|Fs,0|];
aB = DBA(|PB|) + [|FB,0|];
точки T и В расположены аналогично в плоскостях YOZ и XOZ;
ар = аЕ + aW + aN + as + aT + аB + a0p - SpΔxΔyΔz;
b = SCΔxΔyΔz + a0pФ0р;
ρ0p - значение плотности на предыдущем шаге по времени, кг/м3;
Ф0р - значение функции на предыдущем шаге по времени;
Δx, Δy, Δz - шаги вдоль осей OX, OY, OZ соответственно, м;
Δτ - шаг по времени, с.
П.4.3. Используется функция A(|P|) следующем виде (схема со степенным законом изменения числа Пекле внутри контрольного объема):
A(|P|) = [|0,(1 - 0,1|P|)5|]; (П.45)
Операторы типа A(|P|) = [|0,(1 - 0,1|P|)5|] и [|-FT,0|] означают, что при расчете используется большая из величин, разделенных запятой.
П.4.4. Число Пекле Р в выражении (П.45) определяется как отношение F и D, таким образом, Pe = Fe/De и т.д. Расходы F и проводимости D определяются следующим образом:
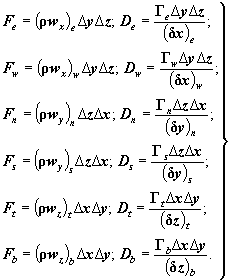 (П.46)
(П.46)
Рис. П.2. Шаблоны контрольных объемов:
а - для основных узлов конечно-разностной сетки; б - для проекции скорости на ось ОХ; в - для проекции скорости на ось ОY
П.4.5. В узлах представленного на рис. П.2, а шаблона конечно-разностной схемы определяются следующие физические величины: температура, плотность, давление, концентрации компонентов газовой среды, коэффициенты тепломассопереноса, теплофизические свойства среды, скорости генерации и диссипации кинетической энергии турбулентности. Для расчета составляющих скорости используется шахматная сетка, т.е. проекция скорости на ось ОY определяется на гранях контрольного объема s и n, перпендикулярных оси ОY (шаблон на рис. П.2, в), проекция скорости на ось ОХ определяется на гранях контрольного объема w и e, перпендикулярных оси ОХ (шаблон на рис. П.2, б), проекция скорости на ось OZ - на гранях контрольного объема b и Т, перпендикулярных оси OZ (контрольный объем определяется аналогично).
Таким образом, конечно-разностные уравнения для составляющих скорости (исходные уравнения (П.2 ¸ П.4)) решаются на соответствующих различных контрольных объемах.
П.4.6. Учитывая, что при пожаре плотность газовой среды помещения существенно изменяется, необходимо использовать уравнение для определения поправки давления в «сжимаемой» форме:
арр'р = аEр'E + аWр'W + аNр'N + аSр'S + аTр'T + аBр'B + b, (П.47)
где: р'i - поправки давления в соответствующих точках.
П.4.7. Поправочные формулы для проекций скорости имеют следующий вид:
wxe = w*xe + de(p'p + p'E); (П.48)
wyn = w*yn + dn(p'p + p'N); (П.49)
wzt = w*zt + dt(p'p + p'T), (П.50)
где: величины с верхним индексом * означают текущие значения величины, а с индексом ' - поправочные значения;
de, dn, dt - величины, получаемые из соответствующих уравнений для компонентов скорости.
П.4.8. Расчёты проводятся на неравномерных конечно-разностных сетках (Δx = var, Δy = var, Δz = var) с переменным шагом по времени, определяемым из условия Куранта [5.26] для всех узлов конечно-разностной сетки:
где: wa - локальная скорость звука, м/с,
kτ < 1 - число Куранта.
П.4.9. Последовательность решения системы алгебраических уравнений, приведенных к «стандартному» виду (П.44), является следующей:
1) задается приближенное поле давления р* = f(x,у,z) (например, давление во всех контрольных объемах равно атмосферному);
2) решаются алгебраические уравнения (П.44), соответствующие уравнениям движения (П.2 ¸ П.4), для получения полей значений скоростей wx* = f1(x,y,z), wy* = f2(x,y,z), wz* = f3(x,y,z);
3) решается уравнение (П.47) для определения поправки давления p' = f4(x,y,z);
4) рассчитывается скорректированное поле давлений р = р* + р';
5) проводится расчет составляющих скорости по формулам (П.48 ¸ П.50);
6) находится решение алгебраических уравнений (П.44), соответствующих уравнениям неразрывности смеси (П.1) и ее отдельных компонентов (П.6), уравнению энергии (П.5), уравнений теплопроводности (П.11 ¸ П.14), а также уравнений (П.19) и (П.20) k-ε модели турбулентности, для определения полей других физических величин (температуры газовой среды и строительных конструкций, концентрации компонентов смеси газов, коэффициентов тепломассопереноса, теплофизических свойств);
7) представление скорректированного давления р как нового р* и возвращение к подпункту 2 настоящего пункта.
Процедура повторяется до тех пор, пока не будет получено сходящееся решение, т.е. отличие параметров газовой среды на соседних итерациях не превышает заранее заданного значения (например, |T(k+1) - Tk| < 0,01 К, где: k+1, k - номера текущей и предыдущей итераций).
П.4.10. Используется неявная конечно-разностная схема [5.26]. При этом система линейных алгебраических уравнений (П.44) решена методом продольно-поперечной прогонки [5.26]. При этом сначала производится решение для одного из выбранных направлений (например, вдоль оси ОХ) с помощью стандартного метода исключения Гаусса. Каждое уравнение системы приводится к виду:
аiФi = biФi+1 + ciФi-1 + di, (П.52)
где: i = 1, 2, ..., Nx - номер точки конечно-разностной схемы вдоль оси ОХ.
Таким образом, физическая величина Фi связана с соседними значениями этой величины Фi-1 и Фi+1. Далее предполагается, что существует следующая зависимость:
Фi = αiФi+1 + βi, (П.53)
где: αi и βi - прогоночные коэффициенты.
Подставляя (П.53) в (П.52), получаем зависимость прогоночных коэффициентов αi и βi от αi-1 и βi-1:
Значения α1 и β1 определяются из граничных условий:
α1 = b1/a1; β1 = d1/a1. (П.56)
Например, в случае граничных условий второго рода при прогонке вдоль оси ОХ для уравнения энергии (П.5) можно записать:
где: ![]() - градиент
температуры по нормали к поверхности ограждающих
конструкций на ее границе;
- градиент
температуры по нормали к поверхности ограждающих
конструкций на ее границе;
Т1, Т2 - температуры в центрах граничного и соседнего контрольных объемов;
Δx - шаг вдоль оси ОХ.
Тогда, в соответствии с уравнениями (П.53) и (П.57) значения α1 и β1 равны:
T1 = α1T2 + β1 = qΔx/λ + T2; α1 = 1; β1 = qΔx/λ. (П.58)
После этого, все прогоночные коэффициенты рассчитываются по формулам (П.54) и (П.55).
Далее из граничных условий на другой границе (i = Nx) определяется величина ФNx и по формуле (П.53) все остальные значения Фi. Например, при граничных условиях второго рода в случае прогонки вдоль оси ОХ (уравнение энергии (П.5)):
TNx-1 = αNx-1TNx + βNx-1 = qΔx/λ + TNx; 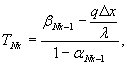 (П.59)
(П.59)
где: TNx, TNx-1 - температуры в центре граничного к поверхности и соседнего контрольных объемов.
Затем выполняется аналогичная прогонка вдоль двух других осей ОУ и OZ с использованием в качестве значений Фi последних в итерационном смысле величин. Описанный алгоритм повторяется вдоль всех осей до тех пор, пока значения функции Фi на соседних итерациях во всех узлах конечно-разностной сетки будут отличаться друг от друга на заранее заданную величину.
П.4.11. Сложная геометрия конструкций и громоздких предметов в помещении задается блокированием в области твердых поверхностей контрольных объемов конечно-разностной сетки, используемой при численном решении на ЭВМ полевой модели, с помощью задания завышенной величины вязкости смеси газов: μ = 1014 кг/(м · с).
Приложение 5.
Параметры горючей нагрузки для жилых и нежилых помещений гражданских зданий
|
№ |
Наименование горючей нагрузки |
Низшая рабочая теплота сгорания Qрн, МДж/кг |
Линейная скорость распространения пламени, wлс, м/с |
Удельная скорость выгорания Ψ0, кг/(м2 · с) |
Удельное дымовыделение Dопг, Нп · м2/кг |
Удельное выделение двуокиси углерода LСО2, кг/кг |
Удельное выделение окиси углерода LСО, кг/кг |
Удельное потребление кислорода LO2, кг/кг |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
Здание 1 - 2 степени огнестойкости; мебель + бытовые изделия |
- |
0,0108 |
0,0145 |
270 |
0,203 |
0,0022 |
-1,03 |
|
2 |
Здание 1 - 2 степени огнестойкости; мебель + ткани |
14,7 |
0,0108 |
0,0145 |
82 |
1,285 |
0,0022 |
-1,437 |
|
3 |
Здание 3 - 4 степени огнестойкости; мебель + бытовые изделия |
13,8 |
0,0465 |
0,0344 |
270 |
0,203 |
0,0022 |
-1,03 |
|
4 |
Здание 3 - 4 степени огнестойкости; мебель + ткани |
14,7 |
0,0465 |
0,0344 |
82 |
1,285 |
0,0022 |
-1,437 |
|
5 |
Здание 1 степени огнестойкости; мебель + ткани (0,75 + 0,25) |
14,9 |
0,0125 |
0,0162 |
58,5 |
1,32 |
0,0193 |
-1,437 |
|
6 |
Здание 3 степени огнестойкости; мебель + ткани (0,75 + 0,25) |
14,9 |
0,04 |
0,0162 |
58,5 |
132 |
0,0193 |
-1,437 |
|
7 |
Кабинет; мебель + бумага (0,75 + 0,25) |
14,002 |
0,042 |
0,0129 |
53 |
0,642 |
0,0317 |
-1,161 |
|
8 |
Помещение, облицованное панелями ДВП |
18,1 |
0,0405 |
0,0143 |
130 |
0,686 |
0,0215 |
-1,15 |
|
9 |
Административное помещение; мебель + бумага (0,75 + 0,25) |
14,002 |
0,022 |
0,021 |
53 |
1,434 |
0,043 |
-1,161 |
|
10 |
Лекарственный препарат; этиловый спирт + глицерин (0,95 + 0,05) |
26,6 |
- |
0,033 |
88,1 |
1,912 |
0,262 |
-2,304 |
|
11 |
Общественные здания; мебель + линолеум ПВХ (0,9 + 1) |
14 |
0,015 |
0,0137 |
47,7 |
1,478 |
0,03 |
-1,369 |
|
12 |
Библиотеки, архивы, книги, журналы на стеллажах |
14,5 |
0,0103 |
0,011 |
49,5 |
1,1087 |
0,0974 |
-1,154 |
|
13 |
Сценическая часть зрительного зала; древесина |
13,8 |
0,0368 |
0,0145 |
57 |
1,57 |
0т024 |
-1,15 |
|
14 |
Верхняя одежда; ворс, ткани (шерсть + нейлон) |
23,3 |
0,0835 |
0,013 |
129 |
0,467 |
0,0145 |
-3,698 |
|
15 |
Резинотехнические изделия; резина, изделия из нее |
36 |
0,0184 |
0,0112 |
850 |
0,416 |
0,015 |
-2,99 |
|
16 |
Окрашенные полы, стены; дерево + краска РХО (0,9 + 0,1) |
14,1 |
0,0151 |
0,0145 |
71,3 |
1,47 |
0,0349 |
-1,218 |
|
17 |
Выставочный зал, мастерская; дерево + ткани + краска (0,9 + 0,09 + 0,01) |
14 |
0,0163 |
0,0152 |
53 |
1,423 |
0,023 |
-1,218 |
|
18 |
Издательство, типографии |
15,4 |
0,004 |
0,0061 |
41 |
0,771 |
0,169 |
-1,158 |
|
19 |
Каюта с синтетической отделкой; дерево + ткани + отделка |
15,8 |
0,0177 |
0,015 |
133,5 |
0,845 |
0,0425 |
-1,249 |
|
20 |
Мебель; дерево + облицовка |
14,4 |
0,0154 |
0,0135 |
84,1 |
1,55 |
0,0367 |
-1,288 |
|
21 |
Промтовары; текстильные изделия |
16,7 |
0,0071 |
0,0244 |
60,6 |
0,879 |
0,0626 |
-2,56 |
|
22 |
Кабельный подвал/лоток; кабели ЛВВГ + АПВГ |
30,7 |
0,0071 |
0,0244 |
521 |
0,65 |
0,1295 |
-2,19 |
|
23 |
Толуол |
40,9 |
- |
0,043 |
562 |
3,677 |
0,148 |
-3,098 |
|
24 |
Ксилол |
41,2 |
- |
0,09 |
402 |
3,657 |
0,148 |
-3,623 |
|
25 |
Бензин А76 |
43,2 |
- |
0,0585 |
256 |
2,92 |
0,175 |
-3,405 |
|
26 |
Керосин |
43,3 |
- |
0,0415 |
438,1 |
2,92 |
0,148 |
-3,341 |
|
27 |
Дизельное топливо; соляр |
45,4 |
- |
0,0425 |
620,1 |
3,163 |
0,122 |
-3,368 |
|
28 |
Радиоматериалы; полиэтилен, стирол, пропил, гетинакс |
34,8 |
0,0137 |
0,0177 |
381 |
0,764 |
0,10 |
-3,312 |
|
29 |
Электротехнические материалы; текстолит, карболит |
20,9 |
0,0125 |
0,0076 |
327 |
0,375 |
0,0556 |
-1,95 |
|
30 |
Теплоноситель; турбинное масло ТП-22 |
41,9 |
- |
0,03 |
243 |
0,70 |
0,122 |
-0,282 |
|
31 |
Электрокабель АВВГ; ПВХ оболочка + изоляция |
25 |
0,0071 |
0,0244 |
635 |
0,398 |
0,109 |
-2,19 |
|
32 |
Электрокабель АПВГ; ПВХ оболочка + полиэтилен |
36,4 |
0,0071 |
0,0244 |
407 |
0,903 |
0,15 |
-2,19 |
|
33 |
Телефонный кабель ТПВ, ПВХ + полиэтилен |
34,6 |
0,0022 |
0,0085 |
556 |
0,903. |
0,124 |
-2,19 |
|
34 |
Сырье для нефтехимии; нефть |
44,2 |
- |
0,0241 |
438 |
3,104 |
0,161 |
-3.24 |
|
35 |
Ацетон |
29 |
- |
0,044 |
80 |
2,293 |
0,269 |
-2,22 |
|
36 |
Этиловый спирт |
27,5 |
- |
0,031 |
80 |
1,937 |
0,269 |
-2,362 |
|
37 |
Лесопильный цех 1 - 3 степени огнестойкости; древесина |
13,8 |
0,0396 |
0,0145 |
57 |
1,57 |
0,024 |
-1,15 |
|
38 |
Лесопильный цех 4 - 5 степени огнестойкости; древесина |
13,8 |
0,0583 |
0,0145 |
57 |
1,57 |
0,024 |
-1,15 |
|
39 |
Цех деревообработки; древесина |
13,8 |
0,022 |
0,0145 |
57 |
1,57 |
0,024 |
-1,15 |
|
40 |
Цех сушки древесины; древесина |
0,138 |
0,0375 |
0,0145 |
57 |
1,57 |
0,024 |
-1,15 |
|
41 |
Производство фанеры; древесина + фанера (0,5 + 0,5) |
16,1 |
0,0191 |
0,0117 |
80,5 |
1,055 |
0,072 |
-1,177 |
|
42 |
Штабель древесины; хвойный + лиственный лес |
13,8 |
0,0585 |
0,0145 |
57 |
1,57 |
0,024 |
-1,15 |
|
43 |
Хвойные древесные стройматериалы; штабель |
13,8 |
0,0585 |
0,0063 |
61 |
1,57 |
0,024 |
-1,15 |
|
44 |
Лиственные древесные стройматериалы; штабель |
13,8 |
0,0585 |
0,014 |
53 |
1,57 |
0,024 |
-1,15 |
|
45 |
Клееные стройматериалы; фанера |
18,4 |
0,0167 |
0,0089 |
104 |
0,54 |
0,121 |
-1,205 |
|
46 |
Сырье для легкой промышленности; хлопок разрыхленный |
16,4 |
0,0445 |
0,0213 |
0,6 |
0,57 |
0,0052 |
-2,3 |
|
47 |
Сырье для легкой промышленности; лен разрыхленный |
15,7 |
0,05 |
0,0213 |
3,37 |
0,36 |
0,0039 |
-1,83 |
|
48 |
Сырье для легкой промышленности; хлопок + капрон (0,75 + 0,25) |
15,7 |
0,028 |
0.0125 |
4,3 |
1,045 |
0,012 |
-3,55 |
|
49 |
Сырье для легкой промышленности; шерсть |
21,8 |
0,028 |
0,02 |
164 |
0,715 |
0,0153 |
-1,759 |
|
50 |
Пищевая промышленность; пшеница, рис, гречиха и мука из них |
17 |
0,005 |
0,008 |
1096 |
0,812 |
0,163 |
-0,968 |
|
51 |
Сырье и изделия из синтетического каучука |
43 |
0,0143 |
0,011 |
212 |
1,408 |
0,15 |
-2,985 |
|
52 |
Склад льноволокна |
15,7 |
0,071 |
0,0213 |
3,4 |
0,36 |
0,0039 |
-1,83 |
|
53 |
Склад хлопка в тюках |
16,7 |
0,0042 |
0,0167 |
0,6 |
0,578 |
0,0052 |
-1,15 |
|
54 |
Склад бумаги в рулонах |
15,1 |
0,005 |
0,008 |
41 |
0,6635 |
0,1077 |
-1,158 |
|
55 |
Провода в резиновой изоляции типа КПРТ, ПТ, ВПРС |
37,8 |
0,005 |
0,1917 |
850 |
0,416 |
0,015 |
-2,99 |
|
56 |
Склад оргстекла (ПММА) |
26,4 |
0,008 |
0,0041 |
78 |
1,795 |
0,1266 |
-2,09 |
|
57 |
Кабель + провода 0,75 (АВВГ, АПВГ, ТПВ) + 0,25 (КПРТ, ПР, ШРПС) |
33,5 |
0,0054 |
0,0622 |
612 |
0,655 |
0,0995 |
-2,89 |
|
58 |
Дерево + лаковое покрытие 0,95 древесина + 0,05 (ФЛ + РХО) |
13,9 |
0,0151 |
0,0225 |
64,1 |
0,724 |
0,0205 |
-1,191 |
|
59 |
Автомобиль: 0,3 (резина, бензин) + 0,15 (ППУ, искусственная кожа ПВХ) + 0,1 эмаль |
31,7 |
0,0068 |
0,0233 |
487 |
1,295 |
0,097 |
-2,64 |
|
60 |
Зал; 0,5 ДВП + 0,1 (ткань, искусственная кожа, ПВХ, ППУ) + 0,2 (дерево с покрытием) |
16,2 |
0,0293 |
0,0123 |
175,6 |
0,817 |
0,041 |
-1,574 |
|
61 |
Тара: древесина + картон + полистирол (0,5 + 0,25 + 0,15) |
20,71 |
0,01 |
0,018 |
155 |
0,97 |
0,094 |
-1,32 |
|
62 |
Упаковка: бумага +картон + поли (этилен + стирол) (0,4 + 0,3 + 0,15 + 0,15) |
23,54 |
0,004 |
0,0132 |
172 |
0,679 |
0,112 |
-1,7 |
|
63 |
Индустриальное масло |
42,7 |
- |
0,043 |
480 |
1,07 |
0,122 |
-1,589 |
|
64 |
Вешала текстильных изделий |
16,72 |
0,0078 |
0,0245 |
61 |
0,879 |
0,063 |
-2,56 |
|
65 |
Отделка; ковролин |
15,397 |
0,021 |
0,013 |
150 |
1,225 |
0,207 |
-2,55 |
|
66 |
Мебель + бумага (0,8) + ковровое покрытие (0,2) |
14,28 |
0,034 |
0,0129 |
72,4 |
0,759 |
0,068 |
-1,439 |
|
67 |
Занавес зрительного зала кинотеатра |
13,8 |
0,05 |
0,0115 |
50 |
0,203 |
0,0022 |
-1,03 |
Приложение 6.
Теплофизические свойства материалов конструкций
|
№ |
Наименование материалов |
Температура t, °С |
Плотность ρ, кг/м3 |
Коэффициент теплопроводности λ, Вт/(мК) |
Удельная теплоемкость с, Дж/(кг · К) |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
Алюминий |
0 100 300 600 |
2700 2690 2650 2550 |
210 205 230 280 |
870 940 1040 1140 |
|
2 |
Аглоперлитобетон |
> 100 |
1670 |
0,7 + 0,7 · 10-5t |
870 + 0,59t |
|
3 |
Альфоль гофрированный |
0 ¸ 550 |
200 |
0,0595 + 2,56 · 10-4t |
- |
|
4 |
Асбест листовой |
- |
900 |
0,075 + 0,0002T |
666 + 0,63T |
|
5 |
Асбестовый картон |
0 ¸ 600 |
1000 ¸ 1300 |
0,157 + 1,86 · 10-4t |
- |
|
6 |
Асбестовая ткань |
0 ¸ 500 |
600 ¸ 700 |
0,123 + 1,86 · 10-4t |
- |
|
7 |
Асбестовый шнур |
0 ¸ 200 |
700 ¸ 900 |
0,14 + 2,32 · 10-4t |
- |
|
8 |
Асбестоцементная напыляемая изоляция |
- |
350 |
0,044 + 0,000186t |
748 + 0,63t |
|
9 |
Асбоцементные сегменты, плиты и скорлупы |
0 ¸ 450 |
400 |
0,087 + 1,28 · 10-4t |
- |
|
10 |
Бетон тяжелый на гранитном щебне |
> 100 |
2220 |
1,42 - 11 · 10-4t |
770 + 0,63t |
|
> 0 |
2330 |
1,3 - 3,5 · 10-4T |
481 + 0,84T |
||
|
11 |
Бетон тяжелый на известняковом щебне |
> 100 |
2190 |
1,25 - 9,6 · 10-4t |
770 + 0,63t |
|
> 0 |
2250 |
1,29 - 5,5 · 10-4T |
481 + 0,84T |
||
|
12 |
Бетон на трепельном заполнителе |
> 0 |
1400 |
0,73 - 1,16 · 10-4T |
710 + 0,48T |
|
13 |
Бетон на щебне из красного кирпича |
- |
1800 |
0,67 |
481 + 0,84T |
|
14 |
Бетон песчаный |
> 100 |
1900 |
1,05 - 5,8 · 10-4t |
770 + 0,63t |
|
> 0 |
2066 |
1,15 - 3,5 · 10-4T |
598 + 0,63T |
||
|
15 |
Бетон поризованный |
> 0 |
1690 |
0,47 |
598 + 0,63T |
|
> 0 |
1433 |
0,48 + 1,16 · 10-4T |
598 + 0,63T |
||
|
16 |
Вата стеклянная |
0 ¸ 450 |
130 |
0,04 + 3,5 · 10-4t |
- |
|
17 |
Вата хлопковая |
20 |
50 |
0,058 |
- |
|
18 |
Вермикулитовые плиты |
0 ¸ 600 |
250 |
0,081 + 2,32 · 10-4t |
- |
|
19 |
Войлок шерстяной |
0 ¸ 90 |
300 |
0,0465 + 1,98 · 10-4t |
- |
|
20 |
Газобетон на молотом песке |
> 100 |
480 |
0,093 + 7 · 10-5t |
920 + 0,63t |
|
> 100 |
750 |
0,186 + 8,1 · 10-4t |
920 + 0,63t |
||
|
> 0 |
480 |
0,041 + 1,9 · 10-4T |
748 + 0,63T |
||
|
> 0 |
750 |
0,164 + 8,1 · 10-5T |
748 + 0,63T |
||
|
> 0 |
1100 |
0,31 |
748 + 0,63T |
||
|
21 |
Грунт глинистый (W = 17,5 %) |
20 |
2100 |
1,4 |
- |
|
22 |
Дерево при потоке тепла: |
|
|
|
|
|
- поперек волокон |
20 |
500 ¸ 600 |
0,163 ¸ 0,174 |
2800 |
|
|
- вдоль волокон |
20 |
500 ¸ 600 |
0,44 ¸ 0,52 |
2800 |
|
|
23 |
Древесные опилки |
20 |
150 ¸ 250 |
0,07 ¸ 0,093 |
- |
|
24 |
Древесностружечные огнестойкие плиты |
0 ¸ 100 |
700 ¸ 800 |
0,105 ¸ 0,174 |
- |
|
25 |
Диатомит молотый |
- |
400 ¸ 500 |
0,091 + 2,8 · 10-4t |
- |
|
26 |
Дюралюминий (Al - 95,5 %, Cu - 4 %, Mn - 0,5 %) |
0 |
- |
160 |
- |
|
20 |
2800 |
165 |
880 |
||
|
100 |
- |
182 |
- |
||
|
200 |
- |
195 |
- |
||
|
27 |
Железо |
20 |
7870 |
67,5 |
452 |
|
200 |
7800 |
61,2 |
482 |
||
|
600 |
7600 |
43,8 |
577 |
||
|
900 |
7500 |
40,0 |
665 |
||
|
28 |
Жароупорный газобетон |
600 |
680 |
430 |
- |
|
29 |
Жароупорный пенобетон: |
|
|
|
|
|
марки 500 |
200 |
500 |
0,192 |
- |
|
|
марки 650 |
200 |
650 |
0,215 |
- |
|
|
31 |
Жаростойкий шлаковатобетон |
100 |
500 ¸ 1000 |
0,116 ¸ 0,232 |
|
|
32 |
Керамзитобетон |
> 100 |
950 |
0,23 + 13,3 · 10-5t |
840 + 0,58t |
|
> 100 |
1030 |
0,256 + 7,5 · 10-5t |
840 + 0,39t |
||
|
> 100 |
1380 |
0,385 + 8,1 · 10-5t |
920 + 0,63t |
||
|
- |
1400 |
0,36 + 8,1 · 10-5T |
707 + 0,48T |
||
|
> 0 |
1500 |
0,30 + 2,3 · 10-4T |
710 + 0,48T |
||
|
- |
1600 |
0,9 + 1,16 · 10-4T |
710 + 0,48T |
||
|
33 |
Керамзитопенобетон |
- |
950 |
0,195 + 1,3 · 10-4T |
680 + 0,59T |
|
34 |
Кирпич глиняный обыкновенный |
- |
1580 |
0,39 + 2,3 · 10-4T |
596 + 0,419T |
|
35 |
Кирпич динасовый |
- |
1900 ¸ 1950 |
0,93 + 7 · 10-4t |
835 + 0,025t |
|
36 |
Кирпич красный |
> 100 |
1580 |
0,455 + 2,32 · 10-4t |
840 + 0,42t |
|
37 |
Кирпич силикатный |
> 100 |
1730 |
0,79 + 3,5 · 10-4t |
840 + 0,63t |
|
- |
1700 |
0,89 - 3,5 · 10-4Т |
674 + 0,60Т |
||
|
38 |
Кирпич шамотный |
- |
1800 ¸ 1900 |
0,835 + 5,8 · 10-4t |
880 + 0,23t |
|
39 |
Кожа |
20 |
- |
0,14 ¸ 0,163 |
- |
|
40 |
Котельная накипь: |
|
|
|
|
|
- богатая гипсом - богатая известью - богатая силикатами |
100 100 100 |
2000 ¸ 2700 1000 ¸ 2500 300 ¸ 1200 |
0,7 ¸ 23 0,15 ¸ 23 0,081 ¸ 0,232 |
- |
|
|
41 |
Латунь (Cu - 70 %, Zn - 30 %) |
0 20 100 300 600 |
8520 |
106 108 110 114 121 |
385 |
|
42 |
Лед |
0 |
920 |
2,23 |
- |
|
43 |
Льняная ткань |
20 |
- |
0,088 |
- |
|
44 |
Маты из штапельного стекловолокна |
- |
60 ¸ 100 |
0,057 + 0,0004T |
582 + 0,63T |
|
45 |
Маты из супертонкого базальтового волокна |
- |
60 - 100 |
-0,0027 + 0,00017T |
582 + 0,63T |
|
46 |
Медь |
20 100 600 1083 |
8930 8900 8700 8510 |
396 392 345 321 |
379 397 456 532 |
|
47 |
Минеральная вата засыпная марки 100 |
0 ¸ 600 |
200 |
0,049 + 1,84 · 10-4t |
- |
|
48 |
Пенопласт плиточный |
20 |
70 ¸ 220 |
0,058 |
- |
|
49 |
Пенополиуретан |
20 |
230 ¸ 260 |
0,0365 ¸ 0,058 |
- |
|
50 |
Пеношамот |
- |
950 |
0,28 + 2,32 · 10-4t |
- |
|
- |
600 |
0,105 + 1,45 · 10-4t |
- |
||
|
51 |
Перлитобетон |
> 100 |
1090 |
0,29 + 1,16 · 10-4T |
840 + 0,58t |
|
> 0 |
1090 |
0,26 + 1,16 · 10-4T |
680 + 0,59T |
||
|
52 |
Перлитовая штукатурка на гипсовом вяжущем |
- |
600 |
0,108 + 8,1 · 10-5T |
786 + 0,49T |
|
53 |
Перлитовая штукатурка на цементном вяжущем |
- |
300 |
0,005 + 2,6 · 10-4Т |
748 + 0,63T |
|
54 |
Перлитовермикулитовая штукатурка |
- |
- |
0,056 + 2,2 · 10-4T |
748 + 0,63T |
|
55 |
Перлитофосфогелиевые плиты |
- |
225 |
0,006 + 2,3 · 10-4Т |
748 + 0,63T |
|
56 |
Песок сухой |
0 ¸ 40 |
1380 |
0,35 |
800 |
|
57 |
Песок влажный (W = 10 %) |
0 ¸ 40 |
1380 |
0,66 |
2000 |
|
58 |
Плиты акмигран |
- |
300 |
0,056 + 1,86 · 10-4Т |
1268 + 1,4T |
|
59 |
Плиты асбестоперлитоцементные плоские облицовочные |
- |
960 |
0,055 + 1,16 · 10-4T |
666 + 0,63T |
|
60 |
Плиты асбосилит |
- |
750 |
0,16 + 9,8 · 10-5T |
520 + 1,47T |
|
61 |
Плиты известково-кремнеземистые теплоизоляционные |
- |
225 |
-0,014 + 2,9 · 10-4T |
677 + 0,59T |
|
62 |
Плиты (маты) из минеральной ваты на синтетическом связующем |
- |
125 |
-0,107 + 5,8 · 10-4T |
582 + 0,63T |
|
63 |
Плиты мраморовидные высокопрочные гипсовые |
- |
2000 |
0,59 - 1,16 · 10-4T |
634 + 0,84T |
|
64 |
Полистирол |
20 |
1100 |
0,16 |
- |
|
65 |
Полиэтилен |
20 |
950 |
0,29 |
- |
|
66 |
Покрытие по стали огнезащитное |
- |
200 |
-0,025 + 2,2 · 10-4T |
1086 + 0,63T |
|
67 |
Пробковые плиты |
20 |
150 - 200 |
0,041 ¸ 0,054 |
1750 |
|
68 |
Олово чистое |
20 |
7300 |
64 |
226 |
|
69 |
Резина: |
|
|
|
|
|
- пористая |
20 |
160 ¸ 400 |
0,05 |
1580 |
|
|
- техническая |
20 |
1500 ¸ 1600 |
0,146 |
1580 |
|
|
70 |
Серебро |
- |
10500 |
410 |
250 |
|
71 |
Свинец |
20 |
11400 |
34,6 |
130 |
|
72 |
Силикатобетон, изготовленный по полугидратной схеме |
> 0 |
1850 |
0,87 - 1,16 · 10-4T |
841 + 0,071T |
|
73 |
Совелит |
0-500 |
500 |
0,104 + 8,9 · 10-5t |
- |
|
74 |
Сплав инвар |
20 |
8130 |
10,7 |
460 |
|
75 |
Сталь арматурная |
> 0 |
7800 |
78 - 0,048t |
310 + 0,48t |
|
76 |
Сталь углеродистая (С - 1 %) |
0 ¸ 800 |
7800 ¸ 7400 |
58 - 0,042t |
470 + 0,21t + 5,0 · 10-4t2 |
|
77 |
Стекло обыкновенное |
20 ¸ 80 |
2500 |
0,75 + 0,00116t |
670 |
|
78 |
Сукно |
20 |
250 |
0,0524 |
- |
|
79 |
Сухая гипсовая штукатурка |
- |
900 |
0,135 + 3,5 · 10-4T |
849 + 0,59T |
|
80 |
Текстолит |
20 |
1300 ¸ 1400 |
0,23 ¸ 0,34 |
1460 ¸ 1500 |
|
81 |
Ткань асбостеклянная |
0 ¸ 500 |
1,2 кг/м2 |
0,123 + 1,86 · 10-4t |
- |
|
82 |
Толь |
20 |
500 - 600 |
0,175 ¸ 0,23 |
- |
|
83 |
Торфоплиты для холодильников |
0 ¸ 100 |
425 |
0,069 + 1,16 · 10-4t |
- |
|
84 |
Чугун (С - 4 %) |
20 |
7270 |
52 |
420 |
|
85 |
Цементно-песчаная штукатурка |
- |
1930 |
0,96 - 4,4 · 10-4Т |
598 + 0,63T |
|
86 |
Шелк |
0 ¸ 93 |
100 |
0,043 ¸ 0,058 |
- |
|
87 |
Шерсть очищенная |
20 |
40 |
0,043 |
- |
|
88 |
Шлак котельный |
- |
700 ¸ 1000 |
0,204 + 2 · 10-4t |
0,75 |
|
89 |
Штукатурка известковая |
0 |
1600 |
0,7 |
840 |
|
90 |
Штукатурка на основе каолинового волокна и цементного вяжущего |
- |
400 |
0,056 + 2,2 · 10-4Т |
748 + 0,63T |
|
91 |
Штукатурка цементная |
20 |
1800 |
1 ¸ 1,15 |
840 |
|
92 |
Фанера березовая клееная |
20 |
800 |
0,175 |
- |
Примечание:
t, T - температуры в °С и К соответственно.
Приложение 7.
Степень черноты поверхностей ряда материалов
|
№ |
Наименование материала |
Температура, °С |
Степень черноты εмат |
|
1 |
2 |
3 |
4 |
|
1 |
Алюминий полированный |
50 ¸ 500 |
0,04 ¸ 0,06 |
|
2 |
Алюминий с шероховатой поверхностью |
20 ¸ 50 |
0,06 ¸ 0,07 |
|
3 |
Алюминий сильно окисленный |
50 - 500 |
0,2 ¸ 0,3 |
|
4 |
Алюминиевая окраска |
50 |
0,5 |
|
5 |
Асбестовая бумага |
40 ¸ 400 |
0,94 ¸ 0,93 |
|
6 |
Асбест листовой |
- |
0,96 |
|
7 |
Асбестовый картон |
20 |
0,96 |
|
8 |
Асбестоцементная напыляемая изоляция |
- |
0,9 |
|
9 |
Асбошифер |
20 |
0,96 |
|
10 |
Бетон на гранитном щебне |
- |
0,625 |
|
11 |
Бетон на известняковом щебне |
- |
0,625 |
|
12 |
Бронза пористая, шероховатая |
50 ¸ 150 |
0,55 |
|
13 |
Бумага |
20 |
0,809 |
|
14 |
Дерево строганое |
20 |
0,8 ¸ 0,9 |
|
15 |
Железо листовое оцинкованное блестящее |
30 |
0,23 |
|
16 |
Железо листовое оцинкованное окисленное |
20 |
0,28 |
|
17 |
Жесть белая старая |
20 |
0,28 |
|
18 |
Керамзитобетон |
- |
0,6 |
|
19 |
Кирпич глиняный обыкновенный |
- |
0,94 |
|
20 |
Кирпич красный, шероховатый |
20 |
0,88 ¸ 0,93 |
|
21 |
Кирпичная кладка, оштукатуренная |
20 |
0,94 |
|
22 |
Кирпич огнеупорный, сильно излучающий |
500 ¸ 1000 |
0,8 - 0,9 |
|
23 |
Кирпич огнеупорный, слабо излучающий |
500 ¸ 1000 |
0,65 ¸ 0,75 |
|
24 |
Кирпич силикатный |
- |
0,9 |
|
25 |
Лак белый |
40 ¸ 100 |
0,8 ¸ 0,95 |
|
26 |
Лак черный блестящий, распыленный на железе |
20 |
0,87 |
|
27. |
Латунь матовая, тусклая |
20 ¸ 350 |
0,22 |
|
28 |
Латунь полированная |
200 |
0,03 |
|
29 |
Маты из супертонкого базальтового волокна |
- |
0,96 |
|
30 |
Маты из штапельного стекловолокна (АТИМОСС) |
- |
0,96 |
|
31 |
Перлитовая штукатурка на гипсовом и цементном вяжущем |
- |
0,8 |
|
32 |
Перлитовермякулитовая штукатурка |
- |
0,9 |
|
33 |
Перлитофосфогелиевые плиты |
- |
0,8 |
|
34 |
Плиты акмигран |
- |
0,9 |
|
35 |
Плиты асбосилит |
- |
0,96 |
|
36 |
Плиты асбестоперлитоцементные плоские облицовочные |
- |
0,9 |
|
37 |
Плиты мраморовидные высокопрочные облицовочные гипсовые |
- |
0,5 |
|
38 |
Плиты известково-кремнеземистые теплоизоляционные |
- |
0,9 |
|
39 |
Плиты (маты) из минеральной ваты на синтетическом связующем |
- |
0,92 |
|
40 |
Покрытие по стали фосфатное огнезащитное |
- |
0,89 |
|
41 |
Сталь листовая, шлифованная |
950 ¸ 1100 |
0,55 ¸ 0,61 |
|
42 |
Стальное литье, полированное |
750 ¸ 1050 |
0,52 ¸ 0,56 |
|
43 |
Сталь листовой прокат |
50 |
0,56 |
|
44 |
Сталь с шероховатой плоской поверхностью |
50 |
0,95 ¸ 0,98 |
|
45 |
Сталь ржавая, красная |
20 |
0,69 |
|
46 |
Сталь окисленная |
200 ¸ 600 |
0,8 |
|
47 |
Сталь листовая с блестящим слоем окиси |
20 |
0,82 |
|
48 |
Сталь сильно окисленная |
50 |
0,88 |
|
49 |
Сталь сильно окисленная |
500 |
0,98 |
|
50 |
Сталь алитированная |
50 ¸ 500 |
0,79 |
|
51 |
Сталь никелированная, матовая |
20 |
0,11 |
|
52 |
Сталь оцинкованная |
20 |
0,28 |
|
53 |
Сталь легированная (8 % Ni; 18 % Cr) |
500 |
035 |
|
54 |
Сажа, нанесенная на твердую поверхность |
50 ¸ 1000 |
0,96 |
|
55 |
Стекло |
20 ¸ 100 |
0,94 ¸ 0,91 |
|
56 |
Смоченная металлическая поверхность |
20 |
0,98 |
|
57 |
Сухая гипсовая штукатурка |
- |
0,86 |
|
58 |
Толь |
20 |
0,91 ¸ 0,93 |
|
59 |
Чугунное литье |
50 |
0,81 |
|
60 |
Цементно-песчаная штукатурка |
- |
0,87 |
|
61 |
Штукатурка на основе каолинового волокна и цементного вяжущего |
- |
0,6 |
|
62 |
Эмаль белая |
20 |
0,9 |
Примечание:
степень черноты внутренней поверхности конструкции со стороны помещения определяется по формуле: ε = (εмат + εсажи)/2,
где: εмат - степень черноты, находящаяся из данной таблицы;
εсажи = 0,96 - степень черноты сажи.
Приложение 8.
Величины огнетушащих концентраций
|
№ |
Огнетушащее вещество |
Огнетушащая концентрация*, % (об.) |
|
1 |
Азот |
35 - 40 |
|
2 |
Аргон |
50 - 55 |
|
3 |
Водяной пар |
30 - 35 |
|
4 |
Гелий |
35 - 40 |
|
5 |
Диоксид углерода |
20 - 40 |
Примечание:
* - примерные значения, зависят от вида горючего вещества
СОДЕРЖАНИЕ